Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 74
Ache o volume do maior cilindro circular reto que possa ser inscrito num cone circular com um raio de e uma altura de .
Passo 1
A questão pede para acharmos o cilindro de maior volume que pode ser inscrito num cone circular com raio e altura . Trata-se de um problema de máximos e mínimos. Desta forma, precisamos achar uma função que queremos maximizar.
Na figura a seguir temos um corte do cilindro de raio e altura inscrito no cone:
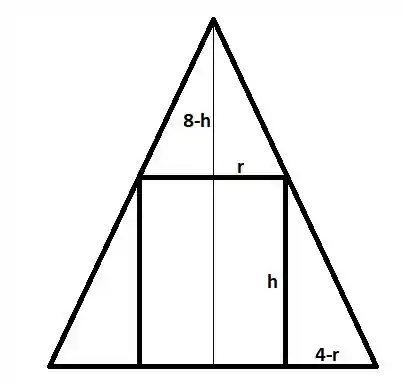
Por semelhança de triângulos, temos que
Multiplicando em cruz:
Portanto,
Assim, temos que
Usaremos essa relação para achar o volume do cilindro como função de !
Passo 2
O volume de um cilindro com raio e altura é
Mas vimos no passo 1 que . Substituindo essa relação:
Assim, queremos achar tal que a função seja máxima no intervalo fechado , já que o raio do cilindro só pode variar entre esses valores.
Passo 3
Como é contínua e o intervalo é fechado, o teorema do valor extremo garante que ela tem máximo e mínimo no intervalo e os candidatos a esses valores são os pontos críticos e os extremos do intervalo. Vamos achar primeiro os pontos críticos no interior do intervalo:
Assim, fazendo , temos que
Entre esses dois pontos, apenas está no interior do intervalo é extremo). Assim, os candidatos a máximo global de são: (ponto crítico), e (extremos do intervalo). Calculando o valor da função nesses pontos:
Assim, o máximo de ocorre em e o mínimo em ou . Assim, é o raio do maior cilindro que pode ser inscrito no cone.
O volume desse cilindro será