Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.4 - Ex. 65
Se e forem as funções cujos gráficos estão mostrados, seja , e . Encontre cada derivada, se ela existir. Se não existir, explique por quê.
Passo 1
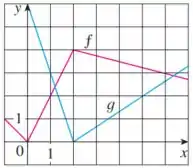
Eaee, belezinha?? Bom... o enunciado nos dá o seguinte gráfico:
Além disso, o enunciado também nos dá as seguintes funções compostas:
Queremos encontrar cada derivada abaixo (se existirem):
Para resolver essa questão podemos apenas pegar a definição da regra da cadeia, onde temos que se:
Então:
Além disso, também vamos usar a ideia de que uma derivada nada mais é do que a inclinação da reta tangente.
Como em , as funções se comportam como retas, fica fácil encontrarmos a inclinação da reta tangente, será a própria inclinação da reta.
A inclinação é dada por:
Sendo e as coordenadas de dois pontos que pertençam a reta.
Agora vamos aplicar!! 😉
Passo 2
Assim, como queremos , ou seja, a derivada de no ponto , é só substituir esse valor na expressão:
Vamos olhar no gráfico o valor de , assim achamos que:
Agora para achar as derivadas nos pontos pedidos vamos ter que achar dois pontos que englobem o valor pedido que sejam lineares de cada função, vamos lá:
Para temos os pontos e , assim, temos que a inclinação é:
Para temos os pontos e , assim, temos que a inclinação é:
Agora é só substituir de volta:
Passo 3
Assim, como queremos , ou seja, a derivada de no ponto , é só substituir esse valor na expressão:
Vamos olhar no gráfico o valor de , assim achamos que:
Entretando não existe, pois ao olharmos o gráfico vemos que é um ponto da função que não possui derivada. Sabemos disso, pois esse ponto possui uma quina. Olhando pela esquerda a função possui uma certa inclinação e olhando pela direita ela possui outra inclinação. De forma, que não podemos inferir uma inclinação única no ponto e tampouco podemos indicar uma derivada para esse ponto.
E portanto, a derivada também não existe.
Passo 4
Assim, como queremos , ou seja, a derivada de no ponto , é só substituir esse valor na expressão:
Vamos olhar no gráfico o valor de , assim achamos que:
Agora para achar as derivadas nos pontos pedidos vamos ter que achar dois pontos que engoblem o valor pedido que sejam lineares de cada função, vamos lá:
Para temos os pontos e , assim, temos que a inclinação é:
Para já calculamos no passo , assim
Agora é só substituir de volta:
Entendeu direitinho?? Responde aee 😉
Resposta
- não existe