Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.4 - Ex. 12
Uma fornalha para a produção de cristais é usada em uma pesquisa para determinar a melhor maneira de manufaturar os cristais utilizados em componentes eletrônicos para os veículos espaciais. Para a produção perfeita do cristal, a temperatura da deve ser controlada precisamente, ajustando-se a potência de entrada. Suponha que a relação seja dada por
onde é a temperatuda em gruas Celsius e é a potência de entrada em watts.
Qual a potência necessária para manter a temperatura em ?
Se for permitida uma variação de a partir dos , qual será o intervalo de potência permitido para a entrada?
Em termos da definição de , de , o que é ? O que é ? O que é ? O que é ? Qual o valor de dado? Qual o valor correspondente de ?
Passo 1
E aí, tudo bem?! Aqui temos a função:
Onde é a temperatura da de uma fornalha, em gruas Celsius e é a potência de entrada em watts.
Sabendo disso temos que responder algumas perguntinhas:
- Qual é o valor de pra ;
- Para uma variação de em torno de qual será o intervalo em torno de ;
- Para a definição de , de quem é cada variável.
A primeira é muito simples, só temos que substituir na fórmula e pra calcular e definir uma função. A resposta vai tá na raiz dessa função! Podemos fazer isso com Bháskara mas vamos usar o método mais simples!
Vamos plotar a função e verificar suas raízes graficamente!
Mas pode isso?!
Nesse problema temos um sinalzinho rosa do lado do enunciado, isso significa que podemos pedir a ajuda de um software gráfico! Que pode ser tanto um programa quanto um site.
A segunda parece muito complicada, mas não é!
Na na letra (b) vamos plotar o gráfico de traçar o intervalo de dado e verificar o intervalo correspondente no eixo . Essa vai ser a nossa resposta!
Finalmente na letra (c) vamos usar a seguinte definição de limite:
Então para todo número , temos , tal que se:
Então:
Aqui o negócio vai ser parar, analisar, pensar e dar os nomes aos bois!
Passo 2
Vamos começar com a letra (a) :
Temos apenas que igualar a expressão a , vamos lá:
Temos então a função:
Plotando o gráfico:
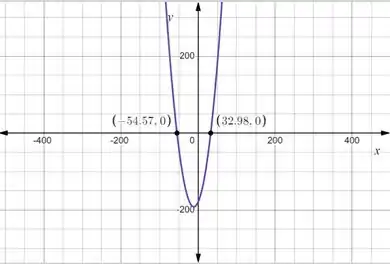
Temos as raízes:
Como a potência tem que ser positiva, então:
Passo 3
Agora a gente vai considerar uma variação de em torno de e queremos saber qual vai ser a variação de . Para isso vamos plotar:
Marcar duas retas horizontais em torno de . Analisar os pontos que essas retas interceptam a curva e checar os valores de correspondentes. As nossas retas serão:
Assim temos:
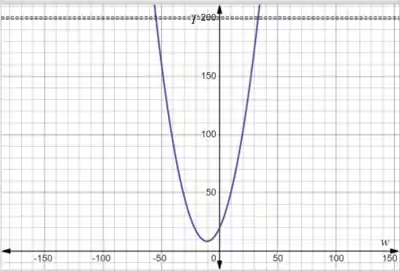
Pra achar onde essas retas interceptam a curva vamos dar um zoom:
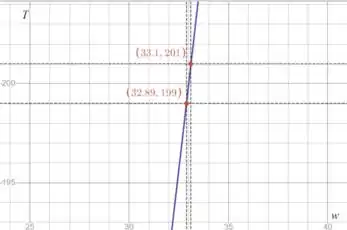
Assim temos que:
Foi a letra (b)!
Passo 4
Agora temos que escrever o limite na forma:
A nossa função é:
Quando nos aproximamos de:
A temperatura tende a:
Então:
Assim:
Agora vamos pensar quem é o e quem é o . Lembrando que:
Então faz sentido inferir que é a tolerância da temperatura que foi dada no enunciado:
E é a tolerância na potência de entrada indicada na letra (b):
Só que aqui o nosso intervalo não é simétrico, então a gente vai calcular a diferença de cada extremo com pra definir o intervalo mais conservador:
O menor valor em módulo aqui é o que vale, então:
Ufaaaa! Acabou!
Resposta
(a) watts
(b)
(c) é a potência de entrada, é a temperatura, é a potência de entrada pedida na letra (a), é a tempetura atingida (, é a tolerância da temperatura igual a , e é a tolerância na potência de entrada igual a .