Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.4 - Ex. 50
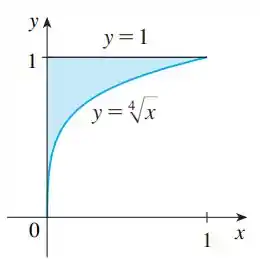
As fronteiras da região sombreada são o eixo , a reta e a curva . Ache a área dessa região escrevendo como uma função de e integrando em relação a (como no Exercício ).
Passo 1
Eaeee, belezinha?? Bom... queremos calcular a área da seguinte região colorida:
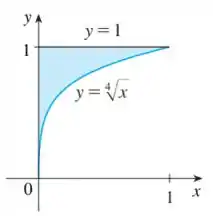
Basicamente vamos fazer um sanduíche, queremos calcular o hamburger (parte colorida), o que segura ele no lugar? Dois pãezinhos que no nosso caso são, o pão de baixo e o pão de cima . Ainda tá faltando uma coisa no nosso sanduíche, a altura sanduíche! Vamos tratar essa altura como o , e vamos olhar o gráfico, ele vai de a , então esse será o nosso limite da integração!
Obs.: a gente também poderia integrar em relação a (aí seria a curva de cima menos a de baixo), mas o enunciado pediu em relação a 😉
Antes de começarmos a calcular, só mais uns detalhes:
O exercício quer em função de , então vamos ter que isolar o , e dentro da nossa integral teremos o (e não se esqueça que teremos ).
E para a primitiva da função, usando uma expressão da Tabela de Integrais Indefinidas:
Depois de encontrar esse primitiva, usaremos o Teorema Fundamental do Cálculo (TFC) para aplicar os limites de integração e assim finalmente encontrar a área!
Agora sim estamos prontos! Bora lá?? 😉
Passo 2
Vamos isolar o em ambas restrições que temos (pãezinhos)
Vamos calcular a área da região que está à direita da reta e à esquerda da curva , para isso precisamos colocar a curva em função de , assim fica (como fazemos para calcular distancia de um ponto a outro):
Vamos primeiro calcular a integral indefinida e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração:
Agora é só aplicar o que vimos no passo 1, simples:
Passo 3
Pronto, agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Como:
E e .
Ficamos então com:
Como a nossa integral é definida não precisamos mais da constante .
Nossa, esse exercício me deu até fome!
Entendeu direitinho?? Responde aee 😉