Para uma função que é contínua em , a Definição diz que a área líquida com sinal entre e o intervalo é:

Dê interpretação geométricas para os símbolos ;

Explique como interpretar o limite dessa definição.

Viiiixee.. vamos começar vendo uma figura pra nos situar:

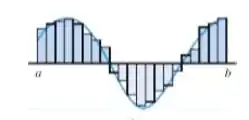
Aqui nós temos uma função, definida num intervalo .

Para representar melhor a área, esse intervalo foi dividido em partes iguais. É isso que o significa: a quantidade de subintervalos em que o intervalo da função foi dividido.

Em cada subintervalo, foram construídos retângulos, com altura igual a em determinado ponto O então é um desses pontos, representado arbitrariamente.

Já o é o comprimento de cada subintervalo.

A explicação para o limite é o seguinte: a medida que cresce, os retângulos vão ficando cada vez mais estreitinhos, e com isso vão preenchendo toooda a área sob a curva, com isso o limite dessa soma calcula a área líquida da função😉