Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.6 - Ex. 4
Para a função cujo gráfico é dado, determine o que se pede
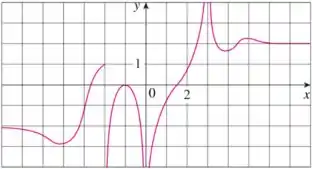
As equações das assíntotas
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade!
Bom galera, nesse exercício queremos encontrar os valores dos limites pedidos com base no gráfico dado na questão.
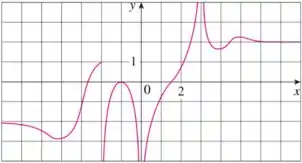
Podemos dizer que o limite de uma função é o valor que a função tende a assumir quando sua variavel se aproxima de um determinado valor.
Então o que vamos fazer é observar o valor que a variavel está se aproximando em cada caso e depois determinar no gráfico o valor que a função tende a assumir nesse ponto.
Sacou? Bora começar!
Passo 2
No item a) temos
(a)
Nesse caso, se aproxima de .
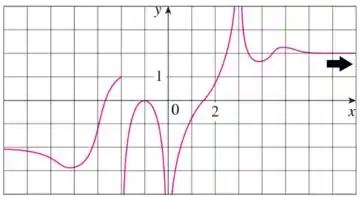
Olhando para o gráfico, podemos ver que conforme o valor de tende a , o valor de se aproxima de , portanto nosso limite é .
Tranquilo até aqui?
Passo 3
Para o item b), temos
(b)
Aqui tende a
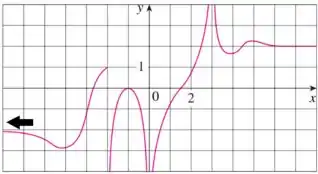
Analisando o outro extremo do gráfico, vemos que quando tende a , a função tende a , logo, nosso limite é .
Show?
Passo 4
No item c), temos
(c)
Agora vamos analisar quando tende a
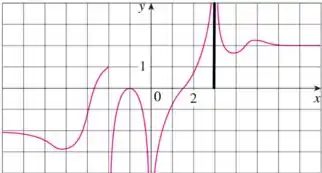
Olhando para o gráfico, podemos ver que conforme o valor de se aproxima de por ambos os lados, o valor de se aproxima de , portanto, nosso limite é .
Está acompanhando?
Passo 5
No item d), temos
(d)
Agora tende a ...
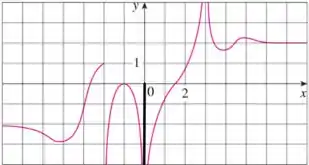
Olhando para o gráfico, podemos ver que conforme o valor de se aproxima de por ambos os lados, o valor de se aproxima de , com isso, podemos dizer que nosso limite é
Sacou?
Passo 6
No item e), chegamos em
(e)
Agora vamos analisar o valor que tende a assumir, quando se aproxima de pela direita .
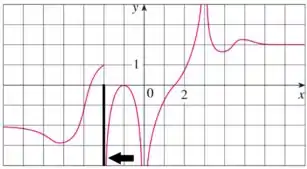
Olhando para o gráfico, podemos ver que conforme o valor de se aproxima de pelo lado direito, o valor de tende a , logo, nosso limite é dado por
Estamos quase lá!
Passo 7
Por fim, o item f), temos
(f) As equações das assíntotas
Vamos começar pelas assíntotas verticais...
Olhando para quando cresce infinitamente, temos as equações verticais das assíntotas, que são
, e
Agora passando para as assíntotas horizontais...
Olhando para quando cresce infinitamente, temos as equações horizontais das assíntotas, que são
e
E aí! entendeu tudo? Responde Aí!
Resposta
Resposta nos passos