Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.2 - Ex. 6
Para a função cujo gráfico é dado, diga o valor de cada quantidade, se ela existir. Se não existir, explique por quê.
Passo 1
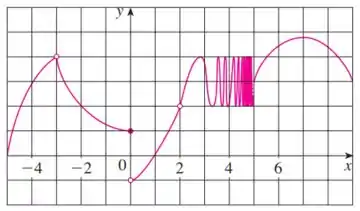
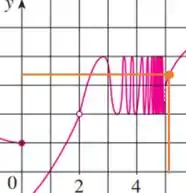
Eaee, belezinha??? Bom... o enunciado nos dá o seguinte gráfico de uma função :
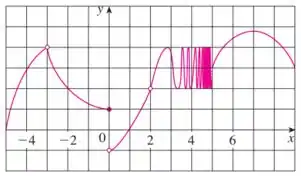
Com esse gráfico, queremos calcular os seguintes limites:
Para isso, devemos ter em mente os limites laterais!!
Mas que limites são esses???
Bom... um limite lateral descreve o comportamento de uma função conforme nos aproximamos de um ponto a partir de diferentes direções no domínio da função.
Geralmente são divididos em limite lateral à esquerda (quando se aproxima pelos valores à esquerda de um número , ou seja, ) e limite lateral à direita (quando se aproxima pelos valores à direita de um número , ou seja, ).
Ahh... vale lembrar que o limite em um ponto só existe se os limites laterais desse ponto forem iguais!! 😉
Agora bora aplicar!! 😉
Passo 2
(a) Vamos fazer primeiro .
Veja o que acontece quando :
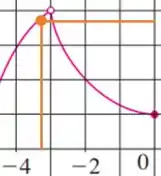
Perceba que quando , .
Logo:
As demais alternativas seguem o mesmo raciocício!!!
Passo 3
(b) Agora para , temos:
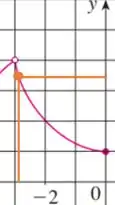
Perceba que quanto mais , , logo:
Passo 4
(c)
Lembra que um limite existe quando seus limites laterais existem e são iguais?
Pois é!!!
Como:
Então:
Passo 5
(d)
A bolinha aberta no gráfico em indica, nesse caso, que a função não está definida em .
Logo, não existe
Passo 6
(e)
Vamos verificar o que acontece quando :
Quando , então, se aproxima de .
Logo:
Passo 7
(f)
Vamos verificar o que acontece quando :
Quando , então, se aproxima de .
Logo:
Passo 8
(g)
Os limites laterais são diferentes, ou seja:
Logo,
Não existe
Passo 9
(h)
Pelo gráfico, vemos que a bolinha fechada para está em .
Logo,
Passo 10
(i)
Agora vamos verificar .
Vamos selecionar um ponto à direita e um ponto à esquerda de :
Pelo gráfico, vemos que os limites laterais tendem a , portanto:
Passo 11
(j)
A bolinha aberta no gráfico em indica, nesse caso, que a função não está definida em .
Logo, não existe
Passo 12
(k)
Vamos verificar .
Quando , temos:
Quando , vemos que , portanto:
Passo 13
(l)
Agora vamos fazer .
Quando , e se aproxima de , oscila loucamente, sem se aproximar de nenhum valor fixo.
Assim, o limite não existe.
Resposta
- não existe
- Não existe
- não existe
- não existe.