Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 6
Para a função cujo gráfico é dado, diga o valor de cada quantidade, se ela existir. Se não existir, explique por quê.
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
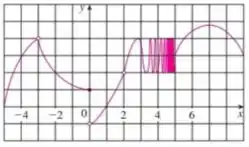
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dado um gráfico de uma função
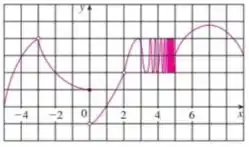
A partir do gráfico, queremos obter os valores de alguns limites em , , e .
Parece complicado?
O limite de uma função nada mais é do que o valor que a função tende a assumir quando tende a um certo valor.
Quando analisamos os limites laterais, quando temos analisamos o lado direito do ponto, quando tende a para valores infinitesimalmente maiores que . Já quando temos , analisamos o valor que a função tende a assumir quando se aproxima de valores infinitesimalmente menores que .
Veja só!
Passo 2
Como temos muito quesitos para analisar, vamos dividir nossa análise por pontos...
Começando pelo ponto .
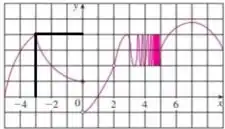
Para valores infinitesimalmente menores que , ou seja, em vemos que tende a . Portanto
Assim como se analisarmos para valores infinitesimalmente maiores que vemos que novamente tende a , ou seja
Aqui, para determinar o limite de quando , embora não exista em , como os limites laterais em convergiram para o mesmo valor, então obrigatoriamente nesse ponto será o mesmo
Pelo gráfico e como observado anteriormente, a função não está definida em , logo
Tranquilo até aqui?
Passo 3
Agora vamos analisar o ponto .
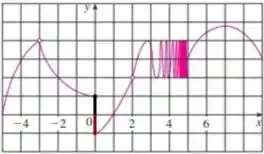
Quando nos aproximando em pela esquerda, vemos que tende a e quando nos aproximamos de pela direita, vemos que tende a , ou seja
Agora, como os limites laterais divergiram, o limite de não existe em
E como tem uma bolinha fechada em e um bolinha aberta em , isso significa que
Show?
Passo 4
O próximo ponto que vamos analisar é em
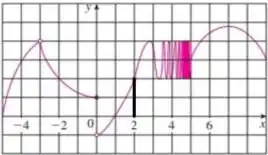
Nesse caso, perceba que tanto nos aproximando pela esquerda, quanto pela direita, vemos que tende a assumir como imagem...
Assim, como os limites laterais convergem para o mesmo valor, o limite no ponto tambem converge para esse valor
Mas como em , temos uma bolinha aberta em , então a função não está definida nesse ponto
Bacana, não é?
Passo 5
Por último, vamos analisar o que acontece em .
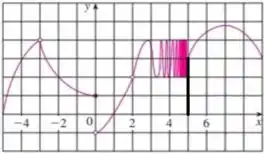
Analisando o gráfico de , podemos observar que quando nos aproximamos pela direita, a função tende a ... logo
Porém, quando nos aproximamos de pela esquerda, a função tende a uma frequência de oscilação tão grande que não podemos definir um ponto de tendencia, logo, o limite diverge
E fim!! O que achou? Responde Aí
Resposta
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)