Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 9
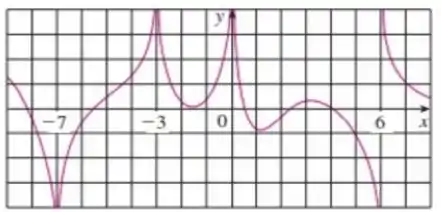
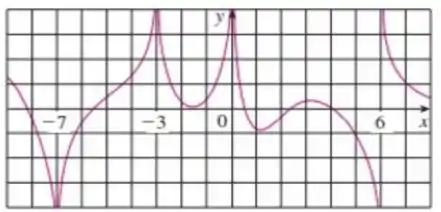
Para a função cujo grafico é mostrado a seguir, determine o seguinte:
- As equações das assintotas verticais.
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Nessa questão, precisamos olhar para o gráfico e tirar as informações que precisamos sobre os limites e limites laterais.
Passo 2
(a) A letra a quer que analisemos o limite para quando chegamos em . E vemos que o limite é infinito porém para valores negativos, então
(b)
Pelo Gráfico, temos quando chegamos em nosso limite vai ao infinito novamente, porém agora iremos ao infinito positivo.
Passo 3
(c)
Pelo Gráfico, temos que quando chegamos ao nosso limite vai novamente ao infinito positivo,
Passo 4
(d)
Pelo Gráfico, temos que quando chegamos a pela esquerda, por valores menores que 6 mas muito proximo, nossa função vai a infinito porem negativo.
Passo 5
(e)
Pelo Gráfico, quando chegamos a agora pela direita, para valores maiores de que 6 porém ainda muito proximo, nossa função vai ao infinito positivo.
Passo 6
(f)
Então, temos que as retas que nos darão as assíntotas verticais da função são os valores para quais nosso limite explode para o infinito, sendo ele positivo ou negativo. No nosso caso são os valores da função são: