Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 8
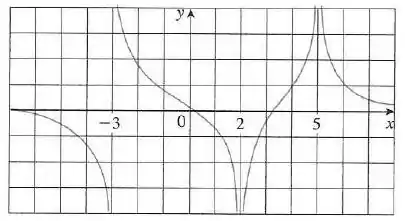
Para a função cujo gráfico é mostrado a seguir, diga quem são:
- As equações das assíntotas verticais
Passo 1
Fala aí! Nosso enunciado quer saber o valor dos limites laterais e do limite a partir do grafico dado, vamos lá então! Vamos analisar isso pelo gráfico, ok?
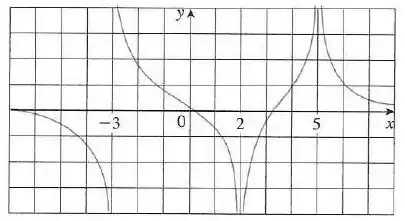
Primeiro na letra a, vamos achar , vemos pelo gráfico que quando tende a nossa função vai tender a infinito, mas para a parte negativa, então vamos ter:
Passo 2
Agora vamos para a letra b, precisar achar , nosso gráfico mostra que quando tende a nossa função vai tender ao infinito, a parte positiva dele, então ficamos com:
Passo 3
Na letra c, temos que achar o .
Pelo gráfico vemos que quando tende a , pelo lado da esquerda, ou seja, temos um , a função vai para valores cada vez menores rapidamente…
Isso diz pra gente então que a tendência da função é o infinito negativo, ok? Vamos ter:
Passo 4
Agora na letra d, temos o .
Pelo gráfico a gente vê que quando tende a , pela direita, ou seja, quando , nossa função tende a ir para valores positivos…
Isso então, quer dizer que a tendência da função é o infinito positivo e sendo assim teremos:
Passo 5
Pra fechar tá faltando só a letra e, ela quer saber quais são as equações das assíntotas verticais… Bom, precisamos então verificar quais os pontos que a função vai apresentar uma assíntota, ok?
Nesses pontos, a função não tá definida e explode para o infinito… Beleza? Olha só, analisando o gráfico, esses são os pontos que nós trabalhamos acima, quando o limite é infinito, positivo ou negativo:
Uhull! Conseguimos!
Resposta
- As equações das assíntotas verticais serão , e .