Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.6 - Ex. 40

Encontre as assíntotas horizontais e verticais

y = (x^2 + 4)/(x^2 - 1)

Passo 1

Para encontrar a assíntota horizontal, tomaremos o limite da função quando x -> +- oo

underset(x -> +- oo)(lim) (x^2 + 4)/(x^2 - 1) = underset(x -> +- oo)(lim) (1 + ((4)/(x^2)))/(1 - ((1)/(x^2))) = (1 + 0)/(1 - 0) = 1

Logo, y = 1 é uma assíntota horizontal

Passo 2

Para encontrar a assíntota vertical é muito simples, devemos pensar o seguinte “Para que ponto que quando x se aproxima a função ‘explode’ para infinito” (podem ser um ou mais pontos), ou seja,

underset(x -> a)(lim) (x^2 + 4)/(x^2 - 1) = +- oo

Para a = +- 1 a condição de assíntota é satisfeita, pois quando mais próximo de 0 é o denominador, maior será o numerador, ou seja, x^2 - 1 -> 0 , ocorre quando x -> +- 1 , logo x = +- 1 é uma assíntota vertical.

Note que os valores de a são calculados igualando o denominador a 0 e encontrando os valores de x .

Passo 3

Mostraremos agora uma comprovação gráfica do resultado obtido

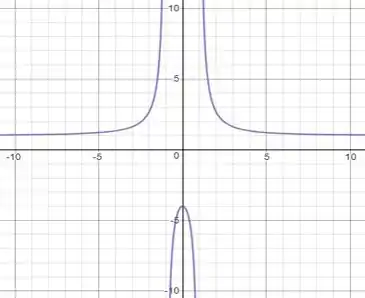
Resposta

y = 1 é uma assíntota horizontal

x = +- 1 é uma assíntota vertical

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 49 a 56, encontre as assíntotas horizontal e vertical e faça um esboço do gráfico da equação 5 4 )2 x y 2 + y 2 - 3 x = 0
Nos exercícios de 49 a 56, encontre as assíntotas horizontal e vertical e faça um esboço do gráfico da equação 55 )x ² y - 2 x 2 - y - 2 = 0 ²
Determine o limite QUOTE _x0001_
Utilize limites para determinar as equações para todas as assíntotas horizontais. y=1-x 2 x 2+1
Utilize limites para determinar as equações para todas as assíntotas verticais. y=x 2+4 x-3