Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.6 - Ex. 43
A função está definida por
Letra a): fazer um esboço do gráfico
Letra b): Em quais números a função é descontínua?
Letra c): Mostrar para cada descontinuidade do item b) por quê não satisfaz a definição 2.6.1
Passo 1
Letra a):
Bom, para isso, temos que esboçar cada função no seu intervalo e juntar tudo!
Como são todas retas, basta identificar os pontos extremos dos intervalos e traçar o segmento de reta que liga esses pontos.
Para o segmento , temos:
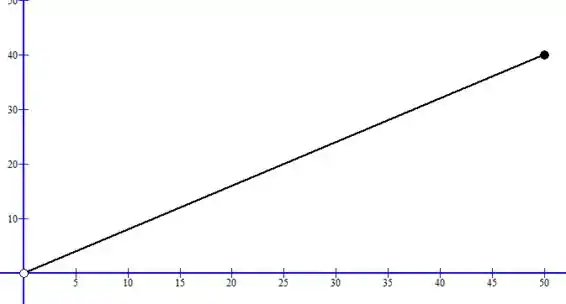
Lembrando que onde a função não foi definida usamos bolinha aberta!
Passo 2
Para o segmento , temos:
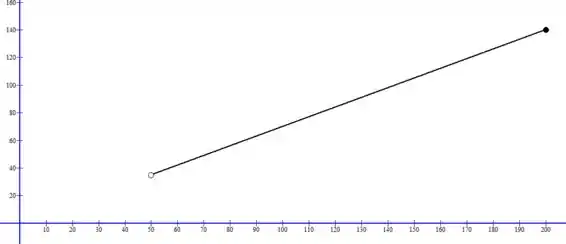
Passo 3
Para o segmento , temos:
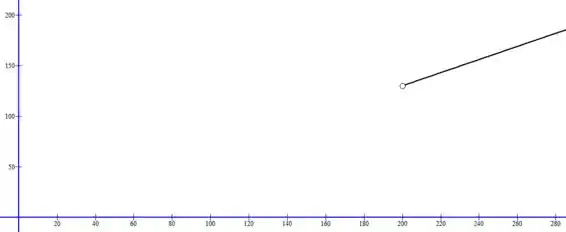
Passo 4
Juntando tudo, temos esse gráfico aqui da função:
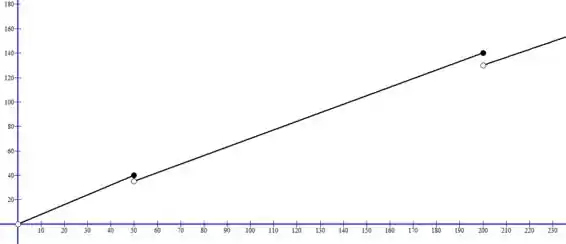
Passo 5
Letra b):
Bom, para determinar os pontos de descontinuidade da função a paetir do gráfico, basta pegar os valores valores de que estão no domínio e o gráfico não é coladinho!
Assim, os valores são exatamente e
Passo 6
Letra c):
Para , não satisfaz a condição de existência de , pois os limites laterais são diferentes.
Resposta
Letra a):
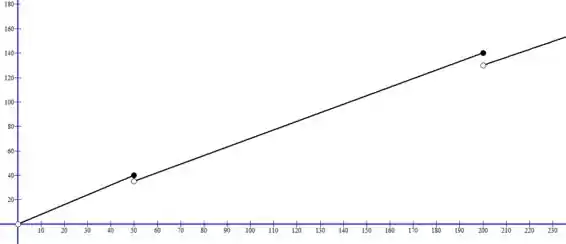
Letra b):
Letra c): Não satisfazem a condição de existência do limite.