Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.6 - Ex. 45
Seja a função definida por
Faça um esboço do gráfico de . Em quais números é descontínua?
Passo 1
Galera, antes de começar a questão vou fazer uma ressalva: A notação em geral não tem um significado universal, mas o livro considera que é a função ‘piso’. Ou seja, quando fazemos , pegamos apenas a parte inteira de cada número positivo, obtendo: . Porém, quando pegamos números negativos, como , se o número for quebrado, pegamos a parte inteira e subtraímos 1, se o número for inteiro, apenas pega a própria parte inteira, obtendo-se .
Assim, vamos fazer um esboço desse gráfico fazendo uma tabela, marcando uns pontos e vendo mais ou menos como eles se comportam num plano cartesiano.
Passo 2
Vou usar alguns números inteiros e outros fracionários pré determinados para montar um gráfico. Os valores serão
Assim, para calcular a f desses valores, precisamos calcular antes , pois a nossa função depende desse número ser par ou ímpar.
que é par, então
que é par, então
que é ímpar, então
que é ímpar, então
que é par, então
que é par, então
que é ímpar, então
que é ímpar, então
que é par, então
No plano, temos então:
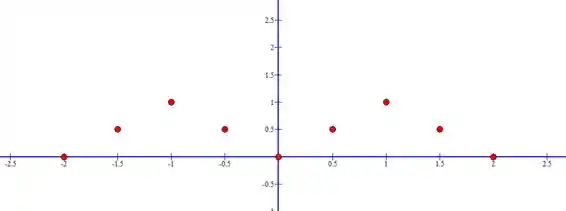
Passo 3
E reparamos que há uma tendência de ir sempre de 0 a 1 e de 1 a 0, seguindo uma espécie de “onda”. Logo, montamos o seguinte gráfico:
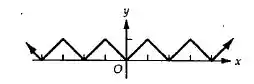
Passo 4
Por fim, observando o gráfico, vemos que essa função não é descontínua em nenhum ponto.
Resposta
Não é descontínua em nenhum ponto.
