Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 8.5 - Ex. 4

A função da densidade:

f x = e 3 - x 1 + e 3 - x 2

É um exemplo de uma distribuição logística.

  1. Verifique que f é uma função densidade de probabilidade.
  2. Encontre P 3 ≤ X ≤ 4 .
  3. Esboce f . O que faz a média aparecer? E quanto a mediana?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos considerar a seguinte função de densidade:

f x = e 3 - x 1 + e 3 - x 2

Vamos verificar se f é uma função de densidade de probabilidade.

Para verificar isto, a função deve satisfazer:

∫ - ∞ ∞ f x d x = 1

Aplicando ao nosso problema, temos:

∫ - ∞ ∞ e 3 - x 1 + e 3 - x 2 d x

Consideremos u = 3 - x , portanto, d u = - d x .

Analisando os limites após a substituição, é possível notar que eles mudam:

Limite inferior:

u = 3 - - ∞ = ∞

Limite superior:

u = 3 - ∞ = - ∞

Passo 2

Vamos aplicar a substituição e os novos limites na integral:

∫ - ∞ ∞ e 3 - x 1 + e 3 - x 2 d x = ∫ ∞ - ∞ e u 1 + e u 2 - d u

Podemos dizer então que:

∫ ∞ - ∞ e u 1 + e u 2 - d u = ∫ - ∞ ∞ e u 1 + e u 2 d u

Resolvendo, temos que:

∫ - ∞ ∞ e u 1 + e u 2 d u = - 1 1 + e u - ∞ ∞

= - 1 1 + e ∞ - - 1 1 + e - ∞

= - 1 1 + ∞ + 1 1 + 0 = - 1 ∞ + 1

Portanto:

∫ - ∞ ∞ e 3 - x 1 + e 3 - x 2 d x = 1

Ficando assim verificada como função densidade de probabilidade.

Passo 3

Item b:

Vamos encontrar o valor de P 3 ≤ X ≤ 4 :

P 3 ≤ X ≤ 4 = ∫ 3 4 f x d x

P 3 ≤ X ≤ 4 = ∫ 3 4 e 3 - x 1 + e 3 - x 2 d x

Consideremos u = 3 - x , portanto, d u = - d x .

Analisando os limites após a substituição, é possível notar que eles mudam:

Limite inferior:

u = 3 - 3 = 0

Limite superior:

u = 3 - 4 = - 1

Substituindo, temos que:

∫ 3 4 e 3 - x 1 + e 3 - x 2 d x = ∫ 0 - 1 e u 1 + e u 2 - d u = ∫ - 1 0 e u 1 + e u 2 d u

Resolvendo, temos que:

∫ - 1 0 e u 1 + e u 2 d u = - 1 1 + e u - 1 0

= - 1 1 + e 0 - - 1 1 + e - 1

= - 1 1 + 1 + 1 1 + e - 1

= - 1 2 + e 1 + e

Portanto:

∫ 3 4 e 3 - x 1 + e 3 - x 2 d x = e - 1 2 e + 1

A probabilidade requerida é:

P 3 ≤ X ≤ 4 = e - 1 2 e + 1

Passo 4

Item c:

O gráfico da função f x = e 3 - x 1 + e 3 - x 2 é mostrado abaixo:

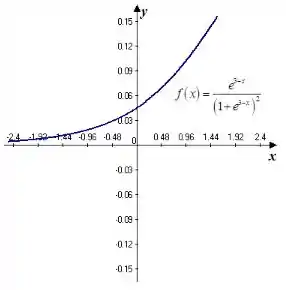
A função média da densidade de probabilidade é:

μ = ∫ - ∞ ∞ x f ( x ) d x

Aplicando ao problema, temos que:

μ = ∫ - ∞ ∞ x e 3 - x 1 + e 3 - x 2 d x

Resolvendo, encontramos:

μ = - x e 3 - x 1 + e 3 - x - ln ⁡ e 3 - x 1 + e 3 - x - ∞ ∞

μ = 3

Passo 5

A função mediana da densidade de probabilidade é:

∫ m ∞ f ( x ) d x = 1 2

Resolvendo, temos que:

∫ m ∞ e 3 - x 1 + e 3 - x 2 d x = 1 2

- e 3 - x 1 + e 3 - x m ∞ = 1 2

Ou seja:

e 3 - m 1 + e 3 - m = 1 2

2 e 3 - m = 1 + e 3 - m

e 3 - m = 1

Portanto:

3 - m = 0

Sendo assim:

m = 3

Resposta

a )   V e r i f i c a ç ã o

b ) P 3 ≤ X ≤ 4 = e - 1 2 e + 1

c ) μ = 3

m = 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Investigar as integrais impróprias seguintes.
Determinar a área sob a curva y = 1 4 - x no intervalo [ 0 ,4 ) .
Dar um exemplo de uma função f , tal que o lim b → + ∞ ⁡ ∫ - b b f x d x existe, mas a integral imprópria ∫ - ∞ ∞ f x d x é divergente.
Verificar se a integral ∫ - ∞ 0 e 5 x d x Converge. Em caso positivo, determinar seu valor.
Investigue a integral imprópria ∫ 7 ∞ 1 x - 5 2 d x