90- Função

1. Faça o gráfico de no intervalo . Como você explica as lacunas no gráfico? Qual a largura dessas lacunas?
2. Agora faça o gráfico de no intervalo . A função não está definida em, mas o gráfico não possui nenhuma interrupção nesse ponto. O que ocorre? Qual valor o gráfico parece atribuir a em ? (Dica: use a regra de l 'Hôpital para determinar lim quando e .)
3. Retomando os gráficos do item (b ), calcule o valor max e min com a maior precisão possível e calcule os valores de x nos pontos em que eles são assumidos.

Letra b)

Se fizermos nós encontramos:

O que é um caso de indeterminação.

A dica para esse tipo de questão é tirar o nos dois lados dessa forma:

Fazendo L’Hopital nessa função temos:

Mas como estamos analisando o limite para o logaritmo natural da função. Logo:

. Logo o limite nesse ponto tende a mesmo sendo um ponto de indeterminação. Ou não...

Letra c)

Fazendo a derivada de para igualarmos a zero e encontrar os seus pontos de máximo e mínimo:

Fazendo a derivada disso temos:

Como não pode ser zero só sobra para quando for zero. Para isso precisamos fazer o método de Newton uma vez que encontrar analiticamente esses números será bastante complicado. Uma função possível de se analisar seria:

O método de Newton tem a seguinte forma:

A derivada de será:

E testando para os pontos e temos (escolhemos esses pontos pois são números fáceis e longe de que seria solução e que como vimos não nos atende).:

Para :

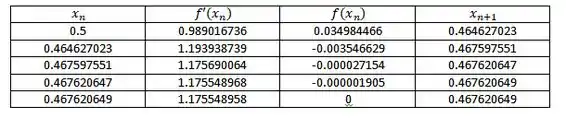
Como nosso apontou zero na calculadora, logo o valor mais preciso de ponto crítico que conseguimos encontrar é

Agora para

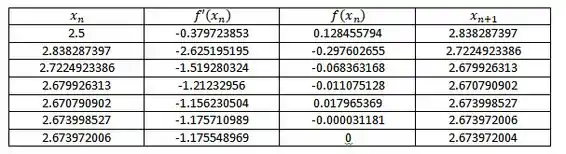
Como nosso erro deu zero, logo o valor mais preciso que encontramos com a calculadora para o outro ponto crítico é de 2.673972004

Note como no primeiro ponto todas as deram positivo, sendo um ponto de mínimo local. Agora para o outro todos os deram negativos, sendo um ponto de máximo.

Plotando o gráfico temos esses pontos: