A função de Fresnel foi definida no Exemplo 3, e seus gráficos estão nas figuras 7 e 8.
- Em que valores de essa função tem valores de máximos locais?
- Em que intervalos a função é côncava para cima?
- Use um gráfico para resolver a seguinte equação, com precisão de duas casas decimais;
Passo 1
Eaee, belezinha?? Bom, temos a seguinte função:
Queremos descobrir em que valores de essa função tem valores de máximos locais, ou seja, quando a derivada muda seu sinal de positivo para negativo.
Além disso, também queremos descobrir os intervalos em que a função é côncava para cima, ou seja, quando a segunda derivada for positiva.
E para isso iremos usar o TFC (Teorema Fundamental do Cálculo), podemos encontrar máximos e mínimos de uma função ao calcular a derivada , encontrar os pontos críticos onde e testar esses pontos para determinar se são máximos ou mínimos.
Ou seja, a derivada de uma integral é a própria função dentro da integral, e vamos iguala-la a , para achar o máximo e mínimo. Sacou? E aí a segunda derivada é só derivarmos a primeira derivada!
E analisaremos os valores da segunda derivada para e .
Por fim, devemos resolver a seguinte integral utilizando um gráfico:
E aí?? Bora lá?? 😉

Passo 2
A função de Fresnel
Tem um máximo local quando e quando muda de um valor positivo para um valor negativo. Podemos calcular pela Parte 1 do Teorema Fundamental do Cálculo:
- Para . Temos um máximo quando
- Para . Temos um máximo local quando
Passo 3
O objetivo é determinar os intervalos onde a função , que é a integral , é côncava para cima, ou seja, onde sua segunda derivada é positiva.
Vamos proceder com a análise detalhada:
Vamos encontrar primeiro :
E aqui usamos a regra da cadeia, lembra dela?
Vamos então derivar a primeira derivada, achando assim e segunda derivada, vai ficar assim:
Agora vamos ter que analisar os domínios!
- Intervalos onde , ou seja, onde é positivo:
- Para , para positivo:
- Para : o que significa que é concava para cima dos intervalos
- Para : o que significa que é concava para cima dos intervalos
- Para , ou seja, para negativo:
- Para :, o que significa que é concava para cima dos intervalos
- Para : , o que significa que é concava para cima dos intervalos
O cosseno é positivo nos intervalos onde está entre e , e entre e , e assim por diante (adicionando múltiplos de).
Portanto, é côncava para cima no intervalo .
Agora vamos analisar os intervalos em que:
Temos
Simplificando e isolado o , temos:
Aqui temos um módulo, mas só estamos procurando para , então:
Ondeé um inteiro positivo
Por exemplo:
Portanto, para cada , temos um intervalo onde é côncava para cima, por exemplo, e assim por diante.
Aqui a análise é um pouco mais complexa porque estamos interessados no comportamento de onde . Isso ocorre nos intervalos:
Para cada inteiro positivo. Simplificando (multiplicando por e dividindo por todos os membros da desigualdade), obtemos:
Aqui temos um módulo, mas só estamos procurando para , então:
Por exemplo:
Portanto, para cada , temos um intervalo onde é côncava para cima, por exemplo, e assim por diante.
Juntando todas as informações, temos que é côncava para cima nos intervalos
Passo 4
Se usarmos o Mapple
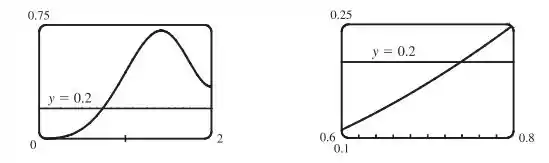
Pelo gráfico vemos que quando .
Entendeu direitinho?? Responde aee 😉