Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 72
A função Seno Integral
É importante em engenharia elétrica
- Trace o gráfico de
- Em que valores de essa função tem valores máximos locais?
- Ache as coordenadas do primeiro ponto de inflexão à direita da origem
- Essa função tem assíntotas horizontais?
- Resolva a seguinte equação com precisão de uma casa decimal
Passo 1
Eaee, belezinha?? Bom.. o enunciado nos dá a seguinte equação:
Queremos plotar o seu gráfico e, para isso, precisaremos de uma calculadora gráfica.
Também temos que calcular os valores de onde essa função tem valores máximos locais, ou seja, onde a sua derivada irá mudar o sinal de positivo para negativo e para isso vamos usar o Teorema Fundamental do Cálculo, podemos encontrar máximos e mínimos de uma função ao calcular a derivada , encontrar os pontos críticos onde e testar esses pontos para determinar se são máximos ou mínimos.
Ou seja, a derivada de uma integral é a própria função dentro da integral, e vamos iguala-la a , para achar o máximo e mínimo. Sacou?
Para achar a segunda derivada, basta derivarmos a primeira derivada, ou seja, a que saiu direto do TFC.
Também devemos encontrar as coordenadas do primeiro ponto de inflexão à direita da origem.
Mas o que é um ponto de inflexão? Bom... trata-se de um ponto em uma curva ou gráfico de uma função onde a concavidade muda de uma parte da curva para outra.
O enunciado ainda nos pede para verificar se essa função tem assíntotas horizontais (lembrando que as assíntotas horizontais são linhas horizontais que uma curva se aproxima à medida que a variável independente se aproxima de mais ou menos infinito.)
Por fim, devemos resolver a seguinte integral:
Muita coisa né?? Então vamos focar cada coisinha dessa em cada passo, combinado??
Bora lá!! 😉
Passo 2
- Usando uma calculadora gráfica, podemos esboçar o gráfico de .
- Para Pequenos: A função cresce rapidamente e de maneira aproximadamente linear.
- Para Médios: A função apresenta oscilações devido ao comportamento da função .
- Para Grandes: As oscilações diminuem em amplitude e a função tende a um valor assintótico, ou seja, tende para uma constante.
Podemos observar isso no gráfico:
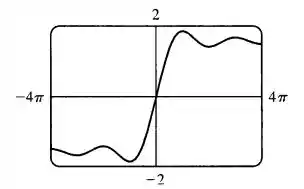
Passo 3
- Para
- Para
Logo, os pontos de máximo são
Passo 4
Resolvendo a expressão no mapple, temos que . Calculando ficamos com
Então o primeiro ponto de inflexão é o ponto
Passo 5
Bom... As assíntotas horizontais são linhas horizontais que uma função se aproxima, mas nunca atinge, à medida que a variável independente se aproxima de infinito positivo ou infinito negativo.
Em outras palavras, à medida que a variável se torna cada vez maior (positiva ou negativa), a função se aproxima, mas nunca atinge, uma linha horizontal específica.
Assim, analisando o gráfico, vemos que possui assíntotas horizontais em .
Além disso, utilizando um comando na calculadora gráfica para encontrar o seguinte limite:
E, como trata-se de uma função ímpar, então:
Assim, também temos as assíntotas horizontais em .
Passo 6
Resposta
(a)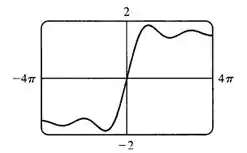 
(b)
(c)
(d) e .
(e)