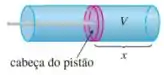
27. Quando um gás se expande em um cilindro de raio , a pressão em um dado momento é uma função do volume: . A força exercida pelo gás no pistão (veja a figura) é o produto da pressão pela área: . Mostre que o trabalho realizado pelo gás quando o volume se expande a partir de para é
Passo 1
E aí, galerinha! 😁

Nesse problema temos que provar que quando um gás de expande de para o trabalho realizado por ele é dado por
Parece complicado? 😬
Sabemos que o trabalho de uma força é dado por
Consideremos um cilindro infinitesimal de raio e espessura . Seu volume será:
Como e são grandezas proporcionais, quando:
Veja só! 😉
Passo 2
Vamos reescrever a equação do trabalho, tendo em vista a mudança de variável:
Se , então
Sacou? Legal, né? Responde Aí! 😎
