- Gere o gráfico de no intervalo
- Encontre a localização exata de todos os pontos críticos e classifique-os como máximos e mínimos relativos, ou nenhum dos dois.
- Confirme os resultados de (b) fazendo o gráfico de no intervalo apropriado.
Passo 1
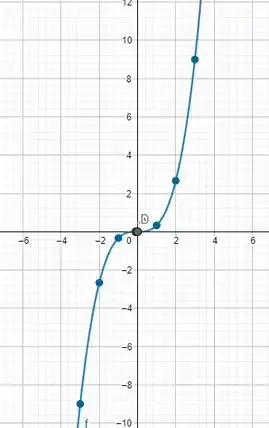
- O exercício pede que usemos uma ferramenta gráfica para formular o gráfico da função, podemos usar ferramentas online, para obter o seguinte gráfico:
- Encontraremos os pontos críticos usando o teste da segunda derivada. Derivando a função temos:
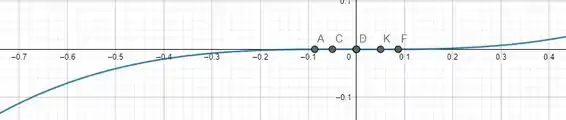
- Nesse passo, o exercício quer apenas observar o gráfico de maneira ampliada.
Passo 2
A raiz da função está em :
Agora, para falidar o teste, calcularemos a segunda derivada e aplicaremos o valor da raíz da primeira derivada na segunda derivada.
Conforme podemos analisar os sinais, observamos que: é um ponto de mínimo relativo, e é um ponto de máximo relativo.
Passo 3
Resposta
é um ponto de mínimo relativo, e é um ponto de máximo relativo.