Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 47
Use um recurso gráfico computacional para gerar os gráficos de e juntos no intervalo e faça uma conjectura sobre a relação entre eles.
Confirme a conjectura em (a).
Passo 1
(a ) O gráfico pode ser dado por:
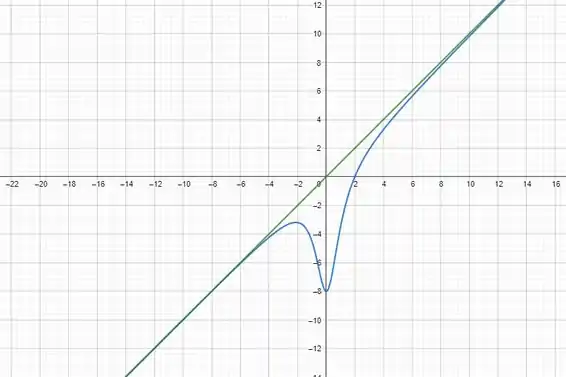
Analisando o gráfico, vemos que as duas função se comportam de maneira semelhante, exceto nos pontos de até .
Passo 2
(b ) Analisando a derivada da função :
Analisando a derivada da função
Quando olhamos o limite de no em , ficamos com:
Como e , a inclinação de é igual a inclinação da reta.
Resposta
Como e , a inclinação de é igual a inclinação da reta.
Exercícios de Livros Relacionados
Nos Exercícios de 13 a 32, faça um esboço do gráfico da função f dada, determinando primeiro o seguinte: os extremos relativos de f ; os pontos de inflexão do gráfico de f ; os intervalos nos quais f
Fazer um esboço do gráfico de f , determinando:. Os extremos relativos de f ;. Os pontos de inflexão do gráfico de f ;. Os intervalos onde f é crescente e aqueles nos quais f é decrescente;. Onde o gr
Fazer um esboço do gráfico de f , determinando:. Os extremos relativos de f ;. Os pontos de inflexão do gráfico de f ;. Os intervalos onde f é crescente e aqueles nos quais f é decrescente;. Onde o gr
Fazer um esboço do gráfico de f , determinando:. Os extremos relativos de f ;. Os pontos de inflexão do gráfico de f ;. Os intervalos onde f é crescente e aqueles nos quais f é decrescente;. Onde o gr
Fazer um esboço do gráfico de f , determinando:. Os extremos relativos de f ;. Os pontos de inflexão do gráfico de f ;. Os intervalos onde f é crescente e aqueles nos quais f é decrescente;. Onde o gr