Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 68
- Use um gráfico para estimar os valores de máximo e mínimo absolutos da função com precisão de duas casas decimais.
- Use os cálculos para encontrar os valores de máximo e mínimo exatos
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a função
E nosso objetivo é usar uma ferramenta gráfica para plotar o gráfico da função no intervalo e estimar os valores de máximo e mínimo e depois obter os mesmos resultados por meio dos cálculos dos pontos críticos.
Parece complicado?
Primeiro vamos plotar o gráfico da função e fazer o que o exercicio pediu: estimar os valores máximos e mínimos dentro do intervalo dado.
Depois, para calcular esses valores vamos usar os pontos críticos de ... pra isso derivamos e igualamos a . Assim vamos verificar quais valores de satisfazem essa igualdade e por fim, aplicamos esses pontos à e comparamos com os valores dos extremos do intervalo.
Bora lá!
Passo 2
Plotando o gráfico com a ajuda de uma ferramenta gráfica, temos
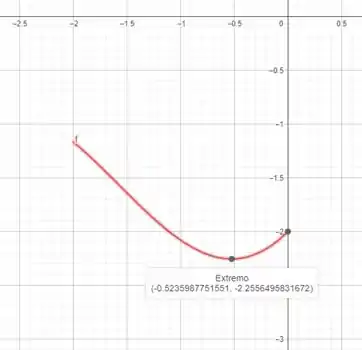
Pelo gráfico podemos ver que o ponto de máximo é o ponto e o mínimo é o ponto
Show?
Passo 3
Agora vamos encontrar os pontos críticos de , pra isso vamos começar calculando a derivada de
Igualando a , temos
O valor corresponde a uma família de valores, mas pertence ao intervalo , então
Tranquilo até aqui?
Passo 4
Agora substituímos em e comparamos com nos extremos do intervalo...
Se , então
Aplicando o limite inferior do intervalo em
Agora o mesmo para o limite superior
Comparando esses resultados, vemos que o máximo aboluto de no intervalo é e o mínimo absoluto é em .
É isso! O que achou? Responde Aí!
Resposta
é um ponto de máximo absoluto e é um ponto de mínimo absoluto.