Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 67
- Use um gráfico para estimar os valores de máximo e mínimo absolutos da função com precisão de duas casas decimais.
- Use os cálculos para encontrar os valores de máximo e mínimo exatos
Passo 1
Oi meus queridos, nessa questão temos a seguinte função:
E vamos usar um recurso gráfico para obter o gráfico dela e ver onde estão os máximos e mínimos absolutos da função.
Depois vamos fazer contra para encontrar esses valores.
O que vamos fazer é derivar a função e igualar a zero:
Os valores que satisfazerem a essa condição são pontos críticos e portanto são possíveis de ser máximo ou mínimo absolutos.
Para saber qual o maior valor entre todos ou o menor valor entre todos, vamos substituir o valor de dos pontos críticos e dos extremos dos intervalos e assim descobrir o máximo e o mínimo absoluto.
Passo 2
Esboçando o gráfico, ficamos com
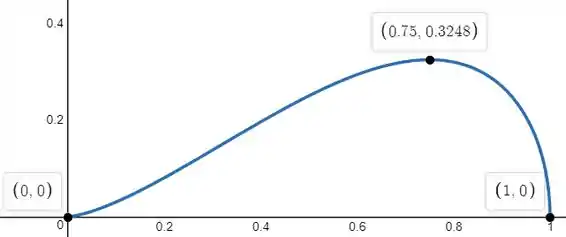
Pelo gráfico, podemos ver que o ponto é um ponto de máximo absoluto e os pontos e são os pontos de mínimo absoluto.
Passo 3
Agora encontrando analiticamente.
Nossa função é:
Vamos aqui aplicar a regra do produto:
Onde e
Dessa forma, temos:
Para encontrar a derivada do último termo, vamos aplicar a regra da cadeia, que é, deriva a função de fora e depois a função dentro
Dessa forma, temos:
Ajeitando isso,
Fazendo o MMC.
Fazendo a multiplicação:
Agora igualando a zero:
Apenas o numerador precisa ser zero.
Fatorando para facilitar:
Passo 4
Aplicando o método do intervalo fechado, necessitamos calcular , e , pois esses são pontos críticos ou são pontos do extremo do intervalo.
Então, é um ponto de máximo absoluto e são pontos de mínimo absolutos.
Resposta
é um ponto de máximo absoluto e são pontos de mínimo absoluto.