Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.3 - Ex. 1
(a) (b)
Passo 1
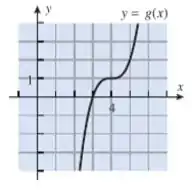
Aqui, só precisamos avaliar como a função se comporta quando tende a (+/-) infinito – veremos se o limite vai existir, ou se, então, a função também segue pra infinito, tornando o limite inexistente.
(a)Aqui a gente observa que, pra valores de em (-) infinito, a função decresce infinitamente. Logo:
Passo 2
(b)De forma análoga que em (a), quando tende a (+) infinito, a função cresce infinitamente. Logo:
Resposta
(a)
(b)
Exercícios de Livros Relacionados
Determine os limites nos Exercícios 23-42.underset(x - - 1)(lim) (sqrt(x^2 + 8) - 3)/(x + 1)
Determine os limites nos Exercícios 11-22.underset(s - 2 // 3)(lim) 3 s ( 2 s - 1 )
Determine os limites nos Exercícios 23-42.underset(x - 2)(lim) (x^2 - 7 x + 10)/(x - 2)
Determine os limites nos Exercícios 11-22.underset(h - 0)(lim) (3)/(sqrt(3 h + 1) + 1)
Suponhamos que a função f ( x ) seja definida para todo valor real de x exceto para x = x 0 . O que pode ser dito sobre a existência de l i m x → x 0 f ( x ) ? Justifique a sua resposta.