Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.2 - Ex. 1
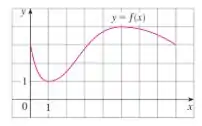
O gráfico de uma função é mostrado. Verifique se satisfaz as hipóteses do Teorema de Rolle no intervalo . Então, estime os valores de que satisfazem a conclusão do Teorema nesse intervalo.
Passo 1
Fala aí! como vai?
Nesse problema foi dado o gráfico
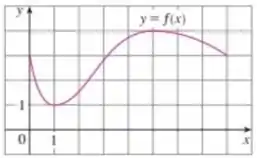
E nosso objetivo é verificar se satisfaz o Teorema de Rolle e se sim, estimar os valores de .
Parece complicado?
O Teorema de Rolle é definido por
Vamos verificar esses três requisitos do teorema na função e estimar os valores de ...
Veja só!
Passo 2
O quesito do teorema diz que a função deve ser continua em todo seu intervalo .
Observando o gráfico vemos que não há nenhuma indeterminação ou assíntota, logo, é sim continua em todo o seu intervalo.
O quesito do teorema diz que é derivável em todo o intervalo.
Podemos observar que não possui nenhuma “quina” e como vimos anteriormente, é continua, logo, tambem é derivável em todo o intervalo.
E por último, o quesito diz que .
Ou seja, começa e termina com a mesma imagem, que analisando o gráfico, vemos que começa e termina em , então esse quesito tambem está verificado!
Tranquilo até aqui?
Passo 3
Pelo Teorema de Rolle, existe pelo menos um valor dentro do intervalo tal que .
Ou seja, no gráfico da nossa função, existe pelo menos um valor dentro do intervalo que possui uma inclinação nula na sua reta tangente, ou seja uma reta horizontal. E isso é o que acontece nos máximos e mínimos de uma função.
Observando o gráfico da função novamente, vemos que
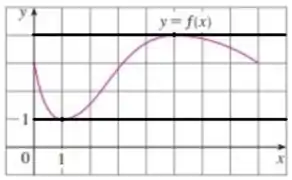
Em e em , , ou seja, a reta tangente possui inclinação ...
É isso! O que achou? Responde Aí!
Resposta
,