Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.9 - Ex. 52
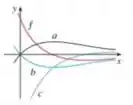
O gráfico de uma função está mostrado. Qual gráfico é uma primitiva de e por quê?
Passo 1
Oie, tudo bem? Vou te ajudar a resolver essa atividade hoje.
A gente tem o gráfico abaixo:
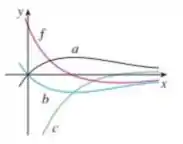
E de rosa, temos a nossa função . Os outros gráficos são os candidatos a gráfico da primitiva de .
Uma função é denominada uma primitiva de num intervalo se:
Queremos descobrir então quem é a primitiva de . Para isso, teremos que relacionar o comportamento de crescimento, decrescimento e de encontros com os eixos ordenados e da nossa função e dos outros gráficos.
Passo 2
Olhando para o gráfico, podemos ver que para valores negativos de em a nossa função é negativa.
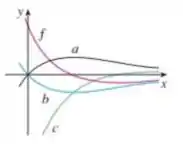
Dessa forma, o gráfico da primitiva deve estar decrescendo. Para os demais valores, a nossa função é positiva, então a nossa função primitiva deverá crescer nesses valores.
Olhando para o gráfico, podemos ver que a única função que satisfaz as condições é a função .
Quando é negativa, está decrescendo. Quando é positiva, está crescendo. Dessa forma, a primitiva da função é a curva .
Resposta
Olhando para o gráfico, podemos ver que a única função que satisfaz as condições é a função . Quando é negativa, está decrescendo. Quando é positiva, está crescendo. Dessa forma, a antiderivada da função é a curva .