Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.7 - Ex. 18
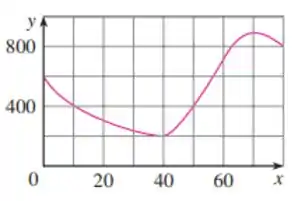
O gráfico da função é mostrado.
(a) Encontre a taxa de variação média de no intervalo [20,60]
(b) Identifique um intervalo o qual a taxa de variação média de é 0.
(c) Qual intervalo possui maior taxa de variação média, [40,60] ou [40,70]?
(d) Calcule o que este valor representa geometricamente?
Passo 1
E aíi, bora resolver essa questãozinha?! Temos esse gráfico aqui:
A primeira coisa que temos que fazer é calcular a taxa de variação média de no intervalo . Pra isso fazemos:
Vamos substituir os valores para o intervalo [20,60]:
Essa foi tranquila, vamos pra próxima!
Passo 2
Agora...em qual intervalo a taxa de variação é igual a zero?!
Pra ser zero temos que ter o numerador igual a zero! Podemos pegar:
Já que:
Então:
Portanto o intervalo é .
Passo 3
O próximo item é a pergunta “Qual intervalo possui maior taxa de variação média, [40,60] ou [40,70]?”
Vamos primeiro encontrar a taxa de variação media para o intervalo
Agora para o intervalo ;
Portanto, vemos que a taxa de variação média de
Passo 4
Agora, pra acabar, é pedido para calcular:
Este valor representa uma reta secante que corta o gráfico nos pontos 10 e 40. O valor negativo representa que y está diminuindo conforme x aumenta, dentro deste intervalo.
Resposta
(a)
(b)
(c) [40,60] > [40,70]