Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.7 - Ex. 16
O deslocamento (em metros) de uma partícula movendo-se ao longo de uma reta é dado pela equação
Onde é medido em segundos.
(a) Encontre as velocidades médias sobre os seguintes intervalos de tempo
(b) Encontre a velocidade instantânea quando .
(c) Faça o gráfico de em função de t e desenha as retas secantes cujas inclinações são as velocidades médias da parte (a), e a reta tangente, cuja inclinação é a velocidade instantânea da parte (b)
Passo 1
Oiee, temos que fazer várias coisinhas nesse problema!
O enunciado nos dá a fórmula do deslocamento de uma partícula ao longo de uma linha reta:
A gente quer (a) velocidade média em diferentes intervalos de tempo:
Vamos calcular os pontos:
Passo 2
Agora, calcularemos as velocidades médias, sabendo que :
Passo 3
Na letra a gente tem que encontrar a velocidade instantânea da partícula em , lembrando que a velocidade é dada pela inclinação reta tangente da posição em um ponto definido que aqui é igual a .
Vamos usar então a seguinte fórmula:
Na letra (a) calculamos:
Substituindo:
Precisamos manipular a equação até a gente poder substituir sem cair em uma indeterminação:
Passo 4
Na letra a gente precisa fazer o gráfico de em função de com várias outras retas!
Lá na letra (a) calculamos várias velocidades médias, essas velocidades são as inclinações das retas secantes que precisamos desenhar aqui! Além disso temos que desenhar a reta tangente com a inclinação que é a velocidade instantânea da letra (b)..
Antes de você sair calculando todas as equações de reta, calma!
Na letra (a) temos dois pontos conhecidos pra cada velocidade, então a gente só precisa identificar esses pontos e traçar uma reta!
Para a reta tangente conhecemos o ponto e sabemos que ela é horizontal, pois sua inclinação é igual a zero, então é só desenhar!
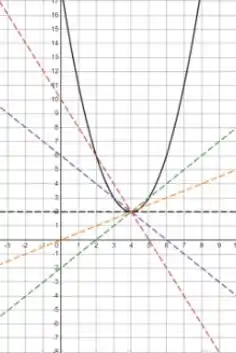
Fazendo os gráficos
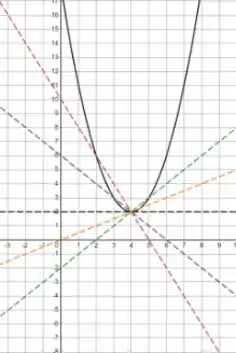
Prontinho!
Resposta
