Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.5 - Ex. 45
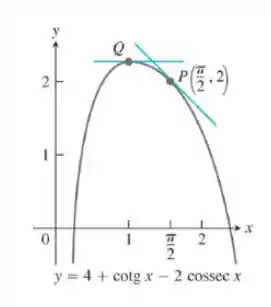
Determine as equações para a tangente à curva em e a tangente horizontal à curva em .
Passo 1
Esta é uma questão bastante interessante. Ela esboça duas possibilidades de trabalho da derivada de uma função e o seu gráfico. Na letra , nos conhecemos as coordenadas do ponto, entretanto, não sabemos qual a inclinação da reta. Desta forma, devemos encontrar a inclinação para só assim obtermos o gráfico da reta tangente. Já na letra , nos conhecemos a inclinação da reta e não conhecemos as coordenadas do ponto . Calma, como assim conhecemos a inclinação da reta???
Bom, a partir do momento em que nos foi informado que a tangente é horizontal no ponto , nos foi dito que a inclinação da reta é igual a 0. Agora sim, sabemos a inclinação. Precisamos então descobrir qual a coordenada do ponto .
Depois disso tudo, a gente entra em um simples questionamento. Como encontramos a inclinação de uma reta tangente a uma curva? É neste exato momento em que entramos com os nossos conhecimentos de cálculo! A função inclinação de uma reta nada mais é a derivada da sua curva. Vamos aos cálculos então!
Passo 2
Antes de começar a resolver qualquer uma das letras, vamos calcular a derivada da função, pois ela será utilizada em ambas as respostas. Sendo assim, temos:
Passo 3
Vamos começar resolvendo a letra . Para isto, devemos calcular a inclinação da reta tangente ao ponto . Assim temos:
Passo 4
Portanto, a inclinação da reta é igual a . Substituindo na equação da reta, temos:
Passo 5
Para descobrir as coordenadas do ponto , vamos resolver a seguinte equação:
Para que a inclinação seja igual a 0, o numerador deve ser igual a 0. Logo,
Como o ponto tem coordenada próxima de 1, conforme pode ser observado pelo gráfico da questão, o valor tal que é:
E as coordenadas do ponto são:
Passo 6
Portanto, a equação da reta tangente horizontal ao ponto é: