Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.2 - Ex. 37
Use um gráfico para encontrar os valores aproximados das coordenadas dos pontos de interseção das curvas dadas. Então encontre (aproximadamente) o volume do sólido obtido pela rotação ao redor do eixo da região limitada por essas curvas.
Passo 1
Vamos desenhar os gráficos dessas duas curvas:
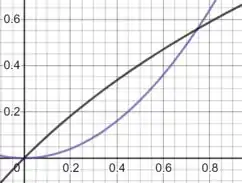
Olhando para esse gráfico, podemos estimar os pontos de interseção das duas curvas:
Passo 2
Quando giramos essa curva em torno do eixo podemos calcular o volume do sólido gerado usando a seguinte fórmula:
E como essa é uma questão que exige o uso da calculadora, vamos calcular essa integral usando um programa:
Resposta
Os pontos de interseção são e . O volume é aproximadamente
Exercícios de Livros Relacionados
(Teorema de Papus para a elipse). Considere o conjunto A de todos os pontos (x, y) tais que x -α 2 a 2 + y - β 2 b 2 ≤ 1 ( a0eb0 ) E situado no semiplano y≥0 . Mostre que o volume do sólido obtido pel
Ache o volume do sólido de revolução gerado pela rotação da região limitada pela curva de y = senh x , pelo eixo x , e pelas retas x = 0 e x = ln 2 , em torno do eixo x .
Ache o volume do solido de revolução descrito quando a região dada da figura for rotacionada em torno da reta indicada.Uma equação da curva na figura é y 2 = x 3 O A C em torno do eixo x
Ache o volume do solido de revolução descrito quando a região dada da figura for rotacionada em torno da reta indicada.Uma equação da curva na figura é y 2 = x 3 O A C em torno da reta A C
Ache o volume do sólido de revolução gerado quando a região limitada pela curva y = x 3 , pelo eixo x e pelas retas x = 1 e x = 2 é rotacionada em torno do eixo x .