Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.9 - Ex. 55

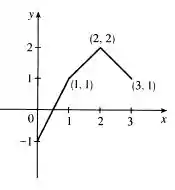
O gráfico de f ' está mostrado na figura. Esboce o gráfico de f se f for contínua e f 0 = - 1 .

Passo 1

Fala aí, galerinha! 😉

Bom, galera... nesse exercício queremos esboçar o gráfico de uma função desconhecida com base em um gráfico de sua derivada sabendo que a função é contínua e que f 0 = - 1 .

Para isso, iremos utilizar os conceitos de antiderivada para encontrar a função que desejamos esboçar.

Veja só! 😁

Passo 2

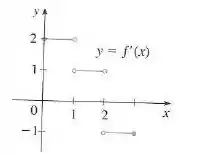
Podemos ver pelo gráfico que a derivada da função se comporta da seguinte maneira

f ' x 2       s e   0 ≤ x < 1 1       s e   1 < x < 2 - 1       s e   2 < x ≤ 3

Dessa forma, para o mesmo comportamento, podemos utilizar a antiderivada em cada uma das partes de f ' para encontrar o comportamento da função que desejamos esboçar

f x = 2 x + C       s e   0 ≤ x < 1 x + D       s e   1 < x < 2 - x + E       s e   2 < x ≤ 3

Tranquilo até aqui? 😉

Passo 3

Como possuímos as condições, podemos encontrar o valor das constantes C ,   D   e   E .

Em f ( 0 ) temos

f 0 = - 1

- 1 = 2 0 + C

C = - 1

Entre ( 1 ,   1 ) e ( 2 ,   2 ) , temos

y = x

Dessa forma, D = 0 . Em ( 3 ,   1 ) , temos

f 3 = 1

1 = - 3 + E

E = 4

Assim, temos

f x 2 x - 1       s e   0 ≤ x < 1 x       s e   1 < x < 2 - x + 4       s e   2 < x ≤ 3

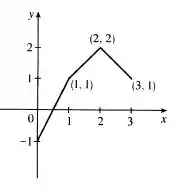
Podemos então esboçar o seguinte gráfico

E aí! o que achou? Responde Aí! 😉

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 23 e 24, use o gráfico para responder às questões.23. Identifique os valores extremos globais de f e os valores de x em que eles ocorrem.
Cada um dos gráficos dos Exercícios 25 e 26 é o gráfico da função posição s = f ( t ) de um corpo que se desloca ao longo de um eixo coordenado (t representa o tempo). Em que tempo aproximadamente, se
A figura mostra dois gráficos, o de uma função y = f x e o de sua derivada f ' x . Identifique cada um. Como você pode saber?
A figura mostra dois gráficos, o de uma função y = f x e o de sua derivada f ' x . Identifique cada um. Como você pode saber?
O gráfico abaixo, mostra o número de coelhos e de raposas em uma pequena população ártica, traçados em função do tempo durante 200 dias. Inicialmente o número de coelhos cresceu devido à sua reproduçã