Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 5
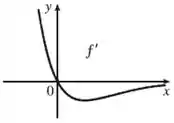
Trace ou copie o gráfico da função dada. (Suponha eixos com a mesma escala.) Use então o método do Exemplo para esboçar o gráfico de .
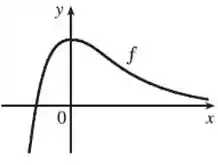
Passo 1
E aí! tudo certinho? 😬
Nesse problema temos que usar o gráfico da função dada para esboçar o gráfico de .
Pra isso vamos usar o método do Exemplo 1 dessa seção do livro, que consiste em traçar retas tangentes na curva e estimar sua inclinação. Isso é baseado no fato de que a derivada num ponto é igual à inclinação da reta tangente naquele ponto.
- Quando temos um ponto de máximo ou mínimo, a reta tangente é horizontal, ou seja, tem inclinação nula. É por isso que nos pontos de máximo e mínimo, a derivada é nula.
- Quando é crescente, é positiva
- Quando é decrescente, é negativa
Então primeiro, vamos plotar todas as interceptações em no gráfico de , nos pontos em que as tangentes no gráfico de forem horizontais
Agora vamos procurar por pontas no gráfico de , se tiver, haverá uma descontinuidade no gráfico de , aqui não temos nenhuma.
Lembremos também que:
Veja só! 😁
Passo 2
Quando , a função é crescente. Olha só como a tangente verde tem inclinação positiva. Em todo esse intervalo, a derivada vai ser POSITIVA.
O mesmo ocorre pra . A inclinação da tangente é negativa, porque a função é descrescente. Então a derivada é NEGATIVA.
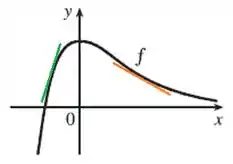
E entre esses intervalos, quando , temos um ponto de máximo. A reta tangente é horizontal e tem inclinação nula. Sendo assim, vai passar pela origem.
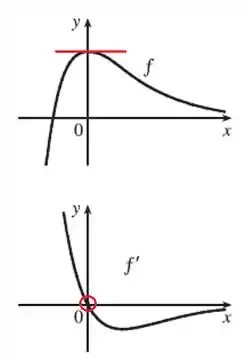
E aí! concorda com isso? Responde Aí! 😁
Resposta
