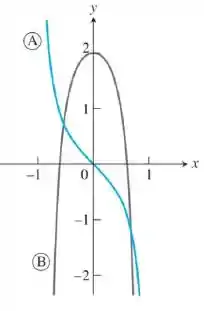
A figura mostra dois gráficos, o de uma função y = f x e o de sua derivada f ' x . Identifique cada um. Como você pode saber?

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 119

A figura mostra dois gráficos, o de uma função e o de sua derivada . Identifique cada um. Como você pode saber?

Passo 1

Vamos dar uma olhada na tal figura que ele falou:

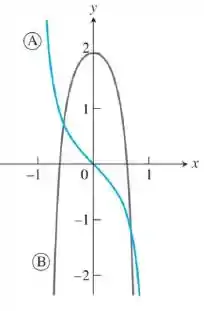
A derivada determina a inclinação da reta tangente certo? Então o que temos que fazer é meio no chute, não vou ficar te enrolando de visões mirabolantes não. Vamos ver se pode ser derivada, se não puder vai ser o .

Olhando o gráfico da , vemos que tem um pedaço negativo e um pedaço positivo. Isso que dizer que vem vezes que a função está com inclinação negativa, ou seja, diminuindo e outra vez com inclinação positiva, ou seja, crescendo.

ENtao o gráfico da deveria ter alguns momentos de subida e outros de decida certo? OOOOOOOOOOOOOOOOOOOPA, não tem, ele é sempre decrescente.

Se invertermos a ideia, vemos uqe é positivo até o e negativo depois dele, ou seja, a deve ser crescente até o e decrescente depois, que é exatamente o que a faz.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o roteiro desta seção para esboçar a curva. y = x - ln ⁡ x

Na teoria da relatividade, a energia de uma partícula é E = m 0 2 c 4 + h 2 ⋅ c 2 γ 2 Em que m 0 é a massa de repouso da partícula, γ é seu comprimento de onda e h é a constante de Planck. Esboce o gr

A Lei de Coulomb afirma que a força de atração entre duas partículas carregadas é diretamente proporcional ao produto das cargas e inversamente proporcional ao quadrado da distância entre elas. A figu

A figura mostra uma viga de comprimento L embutida entre paredes de concreto. Se uma carga constante W for distribuída uniformemente ao longo de seu comprimento, a viga assumirá a forma da curva de de

Esboce o gráfico à mão, usando as assíntotas e as intersecções com os eixos, mas não as derivadas. Então, use seu esboço como um roteiro na obtenção de gráficos (com uma ferramenta gráfica) que mostre