Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 123
O gráfico abaixo, mostra o número de coelhos e de raposas em uma pequena população ártica, traçados em função do tempo durante dias.
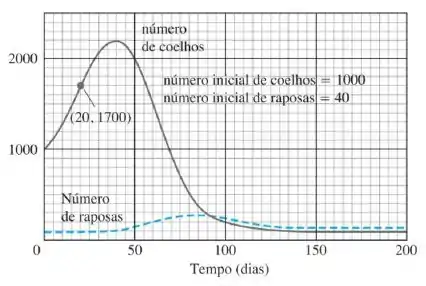
Inicialmente o número de coelhos cresceu devido à sua reprodução. Mas as raposas caçam os colehos e, como o número de raposas cresceu,o nível de coelhos estagnou, e enão caiu.
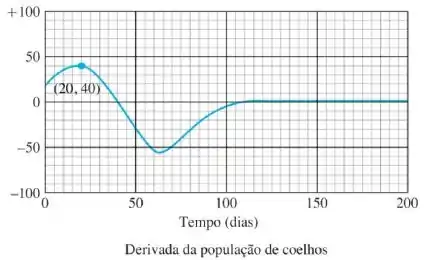
O gráfico abaixo mostra o gráfico da derivada da população de coelhos, construído com o registro dos coeficientes angulares.
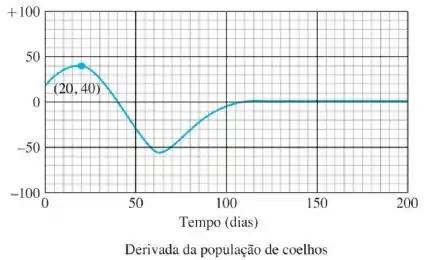
qual é o valor da derivada da população ode coelhos quando o número de coelhos é máximo? E mínimo?
Qual o tamanho da população de coelhos quando a sua derivada é máxima? E Mínimo (valor negativo)?
Passo 1
Basicamente nessa questão, temos que analisar o gráfico que ele deu.
Letra
Vamos olhar os dois juntos, da população e da derivada
o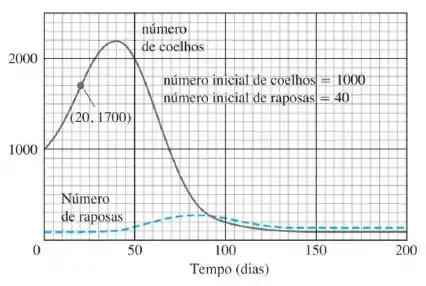 
O número de coelhos é máixmo quando o tempo for , cada quadradinho na horizontal representa dias.
Olhando o gráfico da derivada, o valor dela quando vai ser
O número de coelhos é mínimo quando chega lááááa perto do final do gráfico, depois de dias.
Olhando o gráfico da derivada, ele também vai ser depois de dias.
Passo 2
Letra
A derivada vai ser máxima quando tivermos dias. Olhando o gráfico da população, isso nos diz que ela vai ser .
A derivada vai ser mínima entre o e , vamos estimar que seja o , já que está mais ou menos no meio do quadradinho.
Olhando o gráfico da população, primeiro temos que perceber que cada quadradinho na vertical vale . O valor da função em são mais ou menos quadradinho na vertical depois do , então vai ser
Resposta
Letra
Letra