Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.7 - Ex. 52
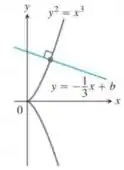
O gráfico de , mostrado na figura a seguir, é chamado de parábola semicúbica. Determine a constante , de modo que a reta intercepte esse gráfico ortogonalmente.
Passo 1
Então pessoal, para que aquela função afim intercepte a parábola ortogonalmente, o que tem que acontecer é que o resultado da multiplicação entre os coeficientes angulares das funções tem que ser , beleza? Em outras palavras:
Mas o que são esses coeficientes angulares? São as derivadas das funções no ponto de incidência. Sendo assim, precisaremos determinar as derivadas implícitas das funções, ok? Bora lá!
Passo 2
Para a função , temos:
Para a função , temos:
Passo 3
Agora que achamos as derivadas, sabendo que os resultados são e , teremos:
Isolando as variáveis, teremos:
Mas como nos foi dado que , temos:
O que implica que as raízes são: e .
Passo 4
Agora que temos os possíveis pontos de interceptação ortogonal entre os gráficos, vamos testá-los! Para , temos:
No entanto, assim como mostrado no passo anterior, não está definido! Sendo assim, o ponto não é o ponto de interceptação ortogonal entre os gráficos. Testando , temos:
Opa, esse ponto está definido, não é mesmo?! Sendo assim, o ponto de interceptação ortogonal entre os gráficos é . Como queremos descobrir a constante , substituindo esses valores lá na função afim, teremos: