Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 8
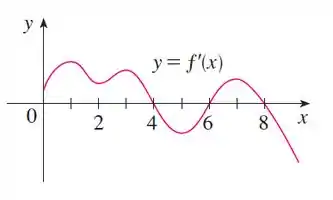
O gráfico da primeira derivada de uma função é mostrado.
- Em que intervalos é crescente? Explique.
- Em que valores de , tem um máximo ou mínimo local. Explique.
- Em que intervalos é côncavo para cima ou côncavo para baixo?
- Quais são as coordenadas dos pontos de inflexão de ? Por que?
Passo 1
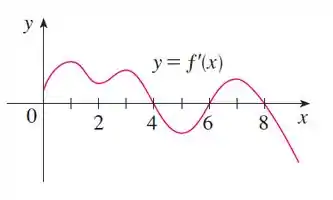
E aíii, tudo bom?! Nesse probleminha temos o gráfico de :
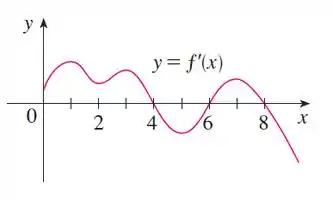
E o enunciado nos pede algumas coisinhas:
- Devemos apontar os intervalos onde é crescente;
- Temos que encontrar os valores de onde é um ponto de máximo ou mínimo local da função .
- Os intervalos onde tem concavidade pra cima ou pra baixo;
- As coordenadas de para os pontos de inflexão de , ou seja, quando a função muda de concavidade.
Essa é uma questão de análise de gráfico, então ela é bem direta, mas temos que ter em mente algumas informações sobre derivadas!
- Se então é crescente e se então é decrescente;
- Se , esse é um ponto crítico, que pode ser um máximo ou mínimo.
- Se é crescente, então e tem concavidade pra cima e no caso contrário. tem concavidade pra baixo
- Por fim, pra saber os pontos onde a concavidade muda, só temos que analisar os intervalos de concavidade que respondemos na letra (c)!
positivo negativo: Temos um ponto de máximo local;
negativo positivo: Temos um ponto de mínimo local;
Eu sei que parece muita coisa, mas vem comigo!
Passo 2
Começamos analisando os intervalos de crescimento e decrescimento de :
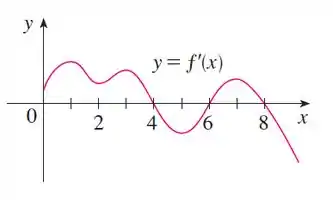
Lembrando que, é crescente quando , olhando o gráfico temos então que é crescente nos intervalos:
e
Passo 3
Agora os pontos de máximo e mínimo locais:
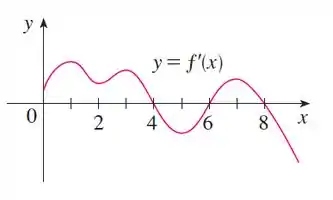
tem um valor máximo local quando troca de sinal de positivo para negativo, vemos no gráfico que isso ocorre em:
e
E tem um valor mínimo local quando troca de sinal negativo para positivo, vemos no gráfico que isso ocorre em:
Passo 4
Agora vamos analisar os intervalos de concavidade, lembrando que é côncava para cima quando , e isso acontece quando é crescente, assim é côncava para cima nos intervalos que a inclinação do gráfico é positiva. No caso contrátrio a concavidade da função é pra baixo!
Analisando o gráfico vemos:
Os intervalos onde é crescente são:
, e
Então nesses intervalos tem a concavidade voltada pra cima. Cuidado pra não confundir crescimento com o sinal positivo da derivada! Em por exemplo, a derivada é negativa, mas ela é crescente!
Agora, os intervalos onde a concavidade da função é virada pra baixo são:
, e
Passo 5
Agora pra acabar! Um ponto de inflexão acontece quando a concavidade da função troca de côncava para cima para côncava para baixo, e vice-versa.
Sabemos que a função é côncava para cima nos intervalos onde a inclinação do gráfico de é positiva, e que é côncava para baixo nos intervalos onde a inclinação do gráfico de é negativa, então vamos olhar a resposta da letra (c):
- Concavidade virada pra cima: , e ;
- Concavidade virada pra baixo: , e .
Então temos pontos de inflexão onde ocorre essa mudança:
Ufaaa!
Resposta
- e
- é crescente em e , e decrescente em
- é côncava para cima em , e , e côncava para baixo em , e