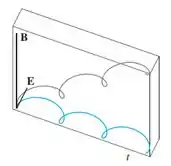
O gráfico de é ilustrado na Figura 12(b), na seção 13.1. Onde você acha que a curvatura é maior. Use um SCA para determinar e fazer o gráfico da função curvatura. Para quais valores de a curvatura é maior?

Analisando a figura, os pontos que parecem ter maior curvatura são os marcados em vermelho

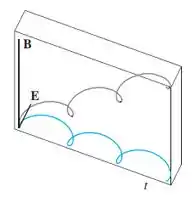
Estes são os pontos mínimos de , e ocorrem quando , já que na formula do , o cosseno é negativo.

Utilizando um software matemático, obtivemos a curvatura

Para encontrar a função , temos que encontrar o módulo do produto vetorial entre e .

Nesta questão não será feito a resolução da equação porque o enunciado pede para utilizarmos um SCA.

Show! Então a função da curvatura fica da segunte forma

E seu gráfico no intervalo

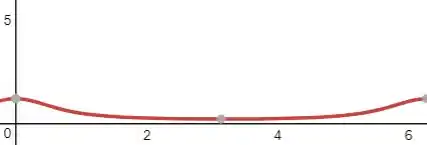
Pelo gráfico da curvatura construído pelo Geogebra, podemos comprovar nosso pensamento, de fato a curvatura é maior quando , que são os pontos .