Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.1 - Ex. 18
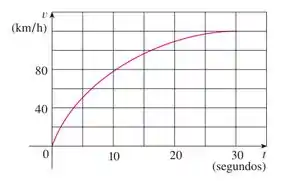
O gráfico da velocidade de um carro em aceleração a partir do repouso até uma velocidade de em um período de segundos é mostrado. Estime a distância percorrida durante esse período.
Passo 1
Eaee, belezinha??
Bom... O enunciado nos dá um gráfico de velocidade em função do tempo que representa um carro saindo do repouso e acelerando até em um período de segundos:
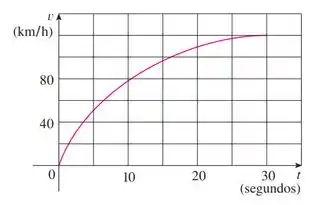
Com base nesse gráfico temos que estimar a distância percorrida pelo carro no intervalo de tempo .
Tem ideia de como fazemos isso?
Para resolver esse problema temos que lembrar que a partir de um gráfico de velocidade, a distância percorrida, em um determinado intervalo, é dada pela area abaixo da curva.
Então para calcularmos a distância percorrida pelo carro vamos usar a formulinha:
Na prática vamos gerar retângulos de altura e largura .
Veja só!
Passo 2
Para resolver esse problema, podemos considerar intervalos de tempo e fazer:
Onde é o ponto médio de cada intervalo e é a distância. O problema aqui é que a nossa velocidade está em enquanto o tempo está em segundo. Sabemos que:
Então:
Tranquilo até aqui?
Passo 3
Pegando os pontos médios de cada intervalo temos:
Nessa questão a gente vai precisar estimar alguns pontos, então eu vou trazer o gráfico mais pra pertinho:
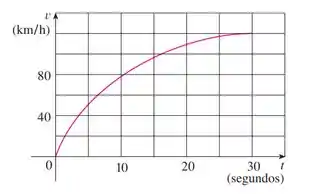
Substituindo:
Então:
Entendeu direitinho?? Responde Aí! 😉