Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 14
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
A questão pede para fazermos um esboço do gráfico da função na janela apropriada. Nesse caso, temos
Nesse caso, precisamos encontrar uma janela retangular de valores de e para plotar o nosso gráfico de forma a demostrar o comportamento da nossa função.
Ela é dada pela soma de que é uma parábola com uma função seno de amplitude .
Para pequeno, a parte oscilatória (seno) é importante, mas a medida que cresce, o termo dado por se torna mais importante e a função vai se aproximando a parábola.
É importante que a nossa janela gráfica mostre isso tudo acontecendo.
Passo 2
Para pequeno, a parte oscilatória é importante. Porém para grande em módulo ela se torna desprezível e a curva se aproxima de uma parábola:
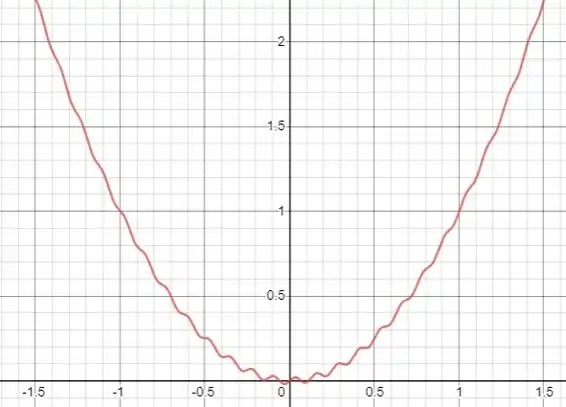
Usando a janela gráfica dada por e já é possível mostrar com clareza o comportamento da função.
Resposta
Janela gráfica:
e