Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 9.6 - Ex. 7
Os gráficos de populações de duas espécies são ilustrados. Use-os para esboçar a trajetória de fase correspondente.
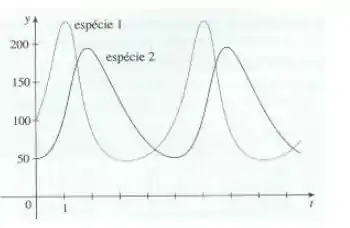
Passo 1
Inicialmente, quando , tínhamos indivíduos da espécie 2 e espécie 1. Quando , o número da espécie 1 atinge seu máximo, em torno de e a espécie 2 tem um crescimento para mais ou menos elementos.
Em um tempo , o número de indíviduos da espécie 1 diminui e o da espécie 2 aumenta até se igualarem em
Agora, em um algum tempo , a espécie 2 atinge seu máximo, em , enquanto a espécie 1 começa decair, ficando com cerca de indivíduos.
Em , a população da espécie 1 atinge seu mínimo, indo para , enquanto a espécie 2 volta a ter 100 indivíduos.
Em as populações voltam a igualar em . Após esse período de tempo o ciclo recomeça a acontecer.
Passo 2
Agora nós precisamos pegar toda a descrição feita e transformá-la em uma trajetória da quantidade de elementos de cada espécie, assim:
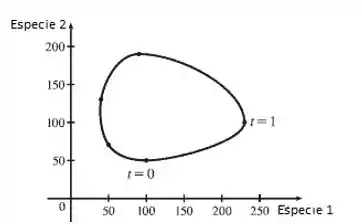
Resposta
Ei, a resposta está no passo a passo :)