Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.3 - Ex. 2
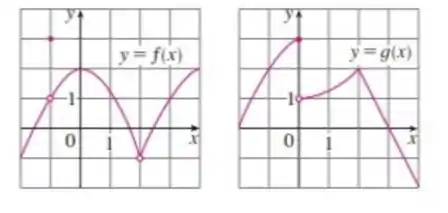
Os gráficos de e são dados. Use-os para calcular cada limite. Caso não exista, explique o por quê.
Passo 1
Letra a
Em todas as questões aqui, vamos primeiro aplicar as propriedades dos limites depois buscar nos gráficos de e abaixo os valores que queremos, ok? Então bora olhar os gráficos:
Pelas propriedades aritméticas do limite, na letra , temos:
Se você olhar bem, vai ver que quando , a função está definida por um ponto a parte do resto da função. Mas não se preocupa, quando calculamos limites, só importa pra onde a função tende quando o tende a .
Dessa forma, vemos que . Pois, tanto pela direita, quanto pela esquerda, conforme nos aproximamos de , se aproxima de . Repetindo a analise para temos que seu limite é 2.
Passo 2
Letra b
Pelo Gráfico e pelas propriedades aritméticas do limite, temos:
Repare como a função tende a valores diferentes quando tende a pela esquerda ou pela direita. Quando isso acontece, dizemos que o limite não existe, assim como a soma:
Passo 3
Letra c
Pelo Gráfico e pelas propriedades aritméticas do limite, temos:
Passo 4
Letra d
Pelo Gráfico e pelas propriedades aritméticas do limite, temos:
Mas como
Não podemos dividir por zero e por isso o limite não existe:
Passo 5
Letra e
Pelo Gráfico e pelas propriedades aritméticas do limite, temos:
Passo 6
Letra f
Agora iremos encontrar o valor de . Mas pelo grafico, esse ponto não esta definido nessa função, basta observarmos que possui ali uma bola aberta, não preenchida significando que este ponto não esta definida na função dada.
Resposta
Os resultados encontrados foram:
- 1
- Não existe