Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.4 - Ex. 7
7. Para o limite
Ilustre a definição 2 encontrando os valores de que correspondam a e
Passo 1
Opaa, tudo joia? Não precisa assustar com a questão, nós vamos resolver passo a passo, olha só!
Aqui nós temos um limite que quando se aproxima de , a expressão se aproxima de 6.
A ideia vai ser usar a definição de limite, como:
Que possui para todo número houver um número tal que:
Se então
Essa é a regrinha, beleza? Então a partir daqui iremos usar essa relação para substituir com os valores dados no enunciado!!
Passo 2
Do enunciado, temos o seguinte:
Plotando o gráfico da nossa função, teremos:
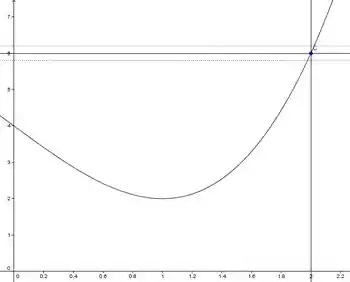
Para :
Logo,
Pelo gráfico temos o seguinte:
Então,
Para o outro ponto:
Então,
Como nossos valores de tem que ficar naquela faixa, vamos pegar o menor . Assim,
Passo 3
Continuando a questão, vamos plotar novamente o nosso gráfico.
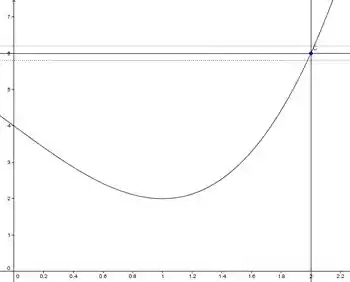
Para :
Logo,
Pelo gráfico temos o seguinte:
Então,
Para o outro ponto:
Então,
Como nossos valores de tem que ficar naquela faixa, vamos pegar o menor . Assim,