Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.4 - Ex. 8
Para o limite
ilustre a Definição encontrando os valores de que correspondam a e .
Passo 1
E aí, pessoal! 😊
Nesse problema queremos ilustrar a definição dessa seção para obter os valores de para e para o limite
Tem ideia de como fazemos isso? 😉
A definição 2 é a definição precisa de limite nos diz que
Calma, não se assusta com essa coisa feia!
Na prática, você só precisa dessas duas inequações que aparecem ali dentro da caixinha rosa:
se então
Vamos aplicar isso na nossa expressão:
então e :
se então
A estratégia é a seguinte, vamos sempre partir da inequação onde aparece o , e vamos mexer nela até aparecer algo parecido com
Assim vamos definir um que atenda essas condições!
Bora começar! 😁
Passo 2
Para , a definição de um limite requer que ache um tal que
Tirando do módulo:
Somando 1 em tudo:
Se plotarmos o gráfico de e traçarmos 2 retas horizontais , conseguirmos enxergar graficamente essa última inequação. Quando que
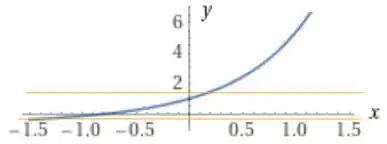
Vamos estimar que aproximadamente:
Vemos que a distância até a extremidade esquerda é , e a distância até a extremidade direita é .
Podemos escolher como o menor desses números, isto é . Embora tenhamos escolhido , qualquer valor menor positivo de também funcionaria.
Tranquilo até aqui? 😊
Passo 3
Para , a definição de um limite requer que ache um tal que
Tirando do módulo ficamos com:
Somando 1 em tudo:
O que implica em:
Se plotarmos o gráfico de , e , vamos achar que:
Vemos que a distância até a extremidade esquerda é , e a distância até a extremidade direita é .
Podemos escolher como o menor desses números, isto é . Embora tenhamos escolhido , qualquer valor menor positivo de também funcionaria.
E fim! Legal, né? Responde Aí! 😎
