Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.3 - Ex. 2
Os gráficos de e são dados. Use-os para calcular cada limite. Caso não exista, explique o porquê.
Passo 1
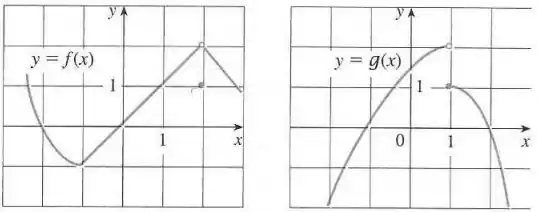
Eaeee, belezinha??? Bom... a questão nos dá esses dois gráficos de duas funções e :
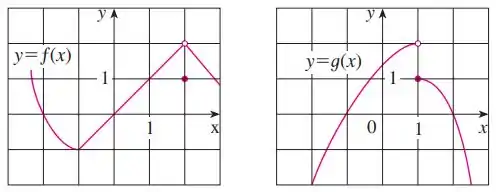
Aqui a gente tem que usar a propriedade dos limites para resolver, iremos de modo geral tentar individualizar o limite de cada função, para que assim possamos olhar no gráfico qual o valor do limite.
As propriedades que iremos utilizar aqui são:
Pois veja, não temos o gráfico da soma, nem do produto das funções, apenas das funções individuais, mas com as propriedades de limites podemos individualizar cada limite e utilizar de forma positiva os gráficos.
E aí?? Bora lá?? 😉
Passo 2
Letra a
Pelas propriedades aritméticas do limite, na letra , temos:
Se você olhar bem, vai ver que quando , a função está definida por um ponto a parte do resto da função.
Mas não se preocupa, quando calculamos limites, só importa para onde a função tende quando o tende a .
Dessa forma, vemos que tanto pela direita, quanto pela esquerda, conforme nos aproximamos de , se aproxima de .
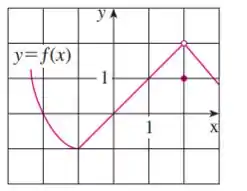
Sendo assim, seu limite é:
Olhando para o gráfico de , quando estiver tendendo a (tanto pela esquerda quanto pela direita), tenderá a .
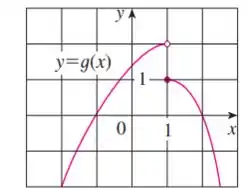
Assim, temos:
Passo 3
Letra b
Pelo Gráfico e pelas propriedades aritméticas do limite, temos:
Repare como a função tende a valores diferentes quando tende a pela esquerda ou pela direita.
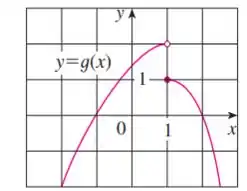
Quando isso acontece, dizemos que o limite não existe, assim como a soma:
Passo 4
Letra c
Pelo Gráfico e pelas propriedades aritméticas do limite, temos:
Olhando para o gráfico de , quando estiver tendendo a (tanto pela esquerda quanto pela direita), tenderá a .
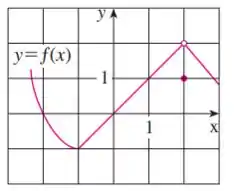
Por outro lado, olhando para o gráfico de , quando estiver tendendo a (tanto pela esquerda quanto pela direita), tenderá a .
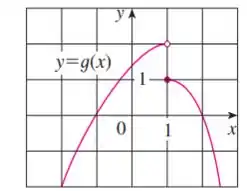
Assim, temos:
Passo 5
Letra d
Pelo Gráfico e pelas propriedades aritméticas do limite, temos:
Mas como quando nos aproximamos de , temos:
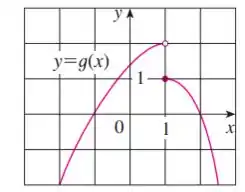
Não podemos dividir por zero e por isso o limite não existe:
Passo 6
Letra e
Pelo Gráfico e pelas propriedades aritméticas do limite, temos:
Mais uma vez, apesar da função valer para , seu limite tende a por ambos os lados e é esse valor que consideramos.
Assim:
Passo 7
Letra f
Pelas propriedades dos limites, temos que:
Como a gente já sabe, pela letra a):
Temos:
Resposta
Os resultados encontrados foram: