Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.4 - Ex. 34
A grande pirâmide do Faraó Quéops foi construída em calcário no Egito ao longo de um período de tempo de anos de a.C. a a.C. Sua base é quadrangular com comprimento de lado de ; sua altura quando foi construída era de . (Foi considerada a estrutura feita pelo homem mais alta do mundo por mais de anos.) A densidade do calcário é de aproximadamente .
- Calcule o trabalho total realizado na construção da pirâmide;
- Se cada operário trabalho durante anos, em dias por ano, e fez pés-lb/h de trabalho ao colocar blocos de calcário no lugar, quantos trabalhadores foram necessários em média para construir a pirâmide?
Passo 1
Opa, temos historinha aqui! O enunciado fala de uma pirâmide do Egito com as seguintes dimensões:
Seu material principal é calcário, com uma densidade de .
Pra esquematizar, vamos assumir que a pirâmide tem lados lisos:
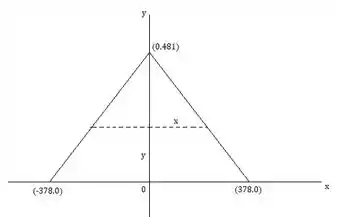
Da figura, para , a equação para o lado é dada por:
Assim, a equação da reta é igual a:
A sessão transversal horizontal tem comprimento igual a e a área dela é igual a:
Uma “fatia” de espessura na altura tem volume igual a e peso . Logo, o trabalho necessário para construir a pirâmide é:
Passo 2
Vamos resolver a integral e encontrar o valor do trabalho a ser realizado.
Assim,
Passo 3
Na letra (b) queremos achar o número de trabalhadores necessários. O trabalho feito por ser escrito como:
Dividindo por temos:
´Prontinho!
Resposta
- ;
- trabalhadores.