Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.6 - Ex. 15
Um tanque com a forma de um hemisfério está colocado de forma que a borda seja uma região circular de raio 6 m e tem água com uma profundidade de 4 m. Ache o trabalho realizado ao se bombear a água para a borda do tanque.
Passo 1
O recipiente desse exercício tem formato de uma semiesfera com a borda circular para cima e queremos bombear a água para fora na altura da borda.
Vamos dar um referencial, o eixo vertical com origem no topo da semiesfera e com sentido positivo para baixo, já que nosso nível de água desce e assim resulta numa maior altura para a água ser levantada.
Passo 2
Vamos descobrir o trabalho contra a gravidade realizado para mover uma camada fina de água de espessura . Pensamos na coluna como uma pilha de camadas bem finas.
Nosso volume da camada terá uma espessura e sua base será dada pela região circular de raio que varia conforme a altura . Vamos encontrar essa função, observe que há uma relação de triângulo, com o sempre fixo:
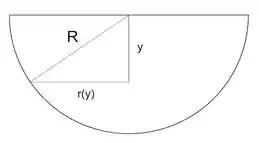
Sabemos que e por Pitágoras podemos fazer essa relação:
E então a base de cada camada será dada pela fórmula da área do círculo:
Passo 3
Vamos para encontrar o trabalho da camada:
O trabalho requerido para levantar cada camada é igual a força vezes a distância a ser percorrida , distância até a borda. Assim nossa equação fica:
Como queremos esvaziar todo o tanque, nosso irá variar de [2, 6], já que nossa origem é na borda e inicialmente está a 2 m abaixo do nível.
Passo 4
Agora vem a menina dos olhos desse exercício, queremos bombear todas as camadas desse tanque e para isso usamos a integral no trabalho:
Simbolicamente o se transforma no da integral. Sabendo que a m/s² e a densidade da água kg/m³, podemos substituir os valores e extrair as constantes da integral:
Passo 5
Agora podemos resolver a integral encontrando as primitivas da função:
E por fim fazer a subtração com os limites da integral: