Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 12.6 - Ex. 1c

c) int (x^4 + x + 1)/(x^3 - x) d x

Passo 1

I = int (x^4 + x + 1)/(x^3 - x) d x

Analisando a integral, vemos que é interessante quebrar em frações parciais. Mas antes temos que dividir os polinômios para o grau do numerador ficar menor do que o do denominador!!

Fazendo a divisão, as coisas ficam assim:

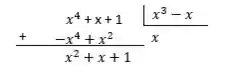
Logo,

x^4 + x + 1 = (x^3 - x) * x + ( x^2 + x + 1 )

Então nossa integral fica assim :

I = int (x^4 + x + 1)/(x^3 - x) d x = ((x^3 - x) * x + ( x^2 + x + 1 ))/(x^3 - x) d x = int (x + (x^2 + x + 1)/(x^3 - x)) d x

Dividindo em duas, temos:

I = int x d x + int (x^2 + x + 1)/(x^3 - x) d x = I_1 + I_2

A primeira fica assim:

I_1 = int x d x = (x^2)/(2) + c_1

A segunda é mais casca grossa!

I_2 = int (x^2 + x + 1)/(x^3 - x) d x = int (x^2 + x + 1)/(x * ( x^2 - 1 )) d x = int (x^2 + x + 1)/(x * (x - 1) * ( x + 1 )) d x

Vamos chamar o que queremos integrar de E e escreve-lo em frações parciais.

E = (x^2 + x + 1)/(x * (x - 1) * ( x + 1 )) = (A)/(x) + (B)/(x - 1) + (C)/(x + 1) ( i )

Deixando os denominadores iguais:

E = (A * (x - 1) * (x + 1) + B * (x) * (x + 1) + C * (x) * (x - 1))/(x * (x - 1) * (x + 1))

Passo 2

Fazendo as contas, temos:

E = (A * (x^2 - 1) + B * (x^2 + x) + C * (x^2 - x))/(x * (x - 1) * (x + 1))

Arrumando a casa:

E = (x^2 * (A + B + C) + x * (B - C) - A)/(x * (x - 1) * (x + 1))

Agora vamos voltar para nossa relação ( i ) :

E = (x^2 + x + 1)/(x * (x - 1) * (x + 1)) = (x^2 * (A + B + C) + x * (B - C) - A)/(x * (x - 1) * (x + 1))

Eita que coisa feia, mas pelo menos é só comparar os coeficientes que acaba essa parte! 😉

x^2 + x + 1 -= x^2 * (A + B + C) + x * (B - C) - A

{[[A + B + C = 1],[B - C = 1],[- A = 1]])

Logo, A = - 1

{[[B + C = 2],[B - C = 1]])

Resolvendo o sistema, temos:

B = (3)/(2) ; C = (1)/(2)

Não esquece: int (1)/(x) d x = ln |x| + c

Passo 3

Agora é só terminar!

I_2 = int (x + 1)/(x * (x - 1) * (x + 1)) d x = int (( - 1 ))/(x) d x + int (((3)/(2)))/(x - 1) d x + int (((1)/(2)))/(x + 1) d x

Tirando as constantes da integral:

I_2 = - 1 * int (1)/(x) d x + (3)/(2) * int (1)/(x - 1) d x + (1)/(2) * int (1)/(x + 1) d x

Resolvendo:

I_2 = - ln |x| + (3)/(2) * ln |x - 1| + (1)/(2) * ln |x + 1| + c_2

Logo, temos:

I = I_1 + I_2 = (x^2)/(2) + c_1 - ln |x| + (3)/(2) * ln |x - 1| + (1)/(2) * ln |x + 1| + c_2

Juntando as constantes:

I = (x^2)/(2) - ln |x| + (3)/(2) * ln |x - 1| + (1)/(2) * ln |x + 1| + c

Resposta

(x^2)/(2) - ln |x| + (3)/(2) * ln |x - 1| + (1)/(2) * ln |x + 1| + c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule.int (2)/(x^3 (x + 2)) d x
Calcule.int (x - 1)/(x^2 (x + 1)^2) d x
Calcule.int (x^3 + 1)/(x^3 - x^2 - 2 x) d x
Calcule.int (x + 1)/((x - 1)^4) d x
Calcule.int (x + 3)/(x^3 - 2 x^2 - x + 2) d x