Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.5 - Ex. 7b
- Seja F um subconjunto do . Dizemos que F é um conjunto fechado se o conjunto de todos os ( x , y ) não-pertencentes a F for aberto. Verifique quais dos conjuntos a seguir são fechados.
b)
Passo 1
Graficamente, essa função ficaria,
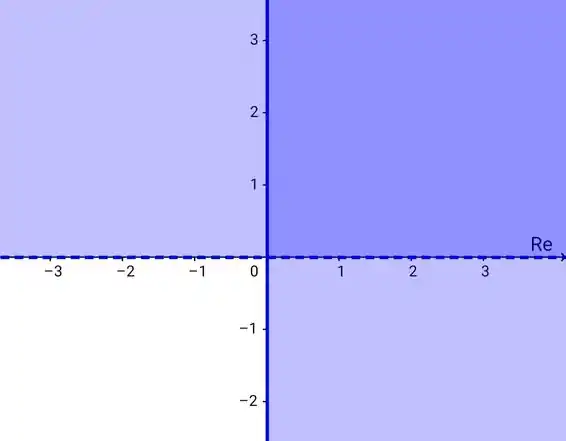
Como tem pontilhado, o conjunto é aberto, ou seja, o conjunto não é fechado.
Resposta
Não é fechado.
Exercícios de Livros Relacionados
Superfície em coordenadas polares Seja f ( r , θ ) = s e n 6 r 6 r , r ≠ 0 1 , r = 0 onde r e θ são coordenadas polares. Encontrea. l i m r → 0 f ( r , θ ) b. f r ( 0,0 ) c. f θ ( r , θ ) , r ≠ 0
Cada um dos Exercícios 75-78 apresenta uma função f (x, y, z) e um número positivo ϵ . Em cada exercício, mostre que existe um δ 0 tal que, para todo número (x, y, z), x 2 + y 2 + z 2δ ⇒ f x , y , z -
Cada um dos Exercícios 69-74 fornece uma função f (x, y) e um número positivo P. Em cada exercício, mostre que existe um δ 0 tal que, para todo (x, y), x 2 + y 2δ ⇒ f x , y - f 0,0ϵ f x , y = x 3 + y
Cada um dos Exercícios 75-78 apresenta uma função f (x, y, z) e um número positivo ϵ . Em cada exercício, mostre que existe um δ 0 tal que, para todo número (x, y, z), x 2 + y 2 + z 2δ ⇒ f x , y , z -
Cada um dos Exercícios 75-78 apresenta uma função f (x, y, z) e um número positivo ϵ . Em cada exercício, mostre que existe um δ 0 tal que, para todo número (x, y, z), x 2 + y 2 + z 2δ ⇒ f x , y , z -