Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 8.3 - Ex. 37
Encontre o centróide da região delimitada pelas curvas e . Esboce a região e desenhe o centróide para verificar se sua resposta é razoável.
Passo 1
Vamos começar o exercício esboçando a região de interesse:
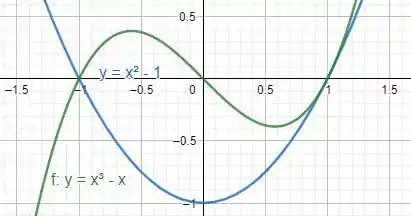
Então, através da figura, podemos verificar que o intervalo de interesse será de , com a função acima da função durante todo o intervalo, então, a área dessa região pode ser dada pela integral:
Resolvendo a integral:
Substituindo os limites de integração, temos:
E, simplifcando a expressão, a área é:
Passo 2
Para calcularmos o centro de massa do sistema, precisamos das coordenadas e dele, então, começando por , temos:
E, resolvendo a integral:
Substituindo os limites de integração:
E, simplificando a expressão:
Passo 3
Agora para a coordenada , calculamos de uma maneira um pouco diferente:
Em que, é a curva que fica acima e é a curva que fica abaixo, então, substituindo os valores de e :
Abrindo os produtos notáveis:
Resolvendo a integral, temos:
Substituindo os limites de integração:
E, simplificando a expressão, temos:
Logo, o centróide é:
O gráfico com o centróide desenhado é mostrado a seguir:
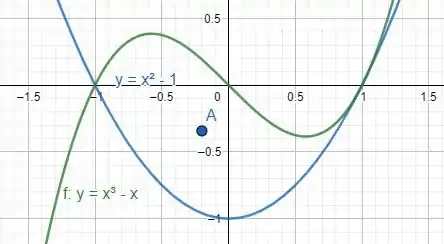
O que parece ser uma posição razoável para o centróide da região.