Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 1.2 - Ex. 4b
Uma haste, presa na origem do plano , ocupa a posição da reta . A haste intercepta a reta no ponto e a elipse no ponto . Quando varia, o vértice do triângulo retângulo decresce uma curva.
Passo 1
Vamos começar substituindo o parâmetro das equações paramétricas por alguns valores do conjunto :
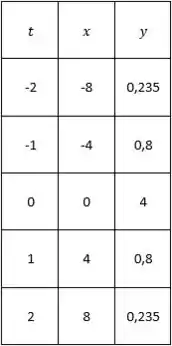
Resposta
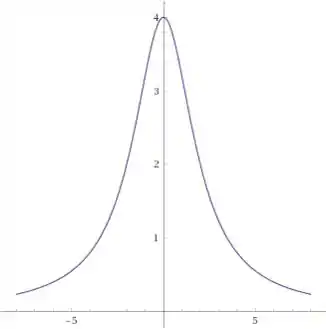
Esboçando a curva descrita pelas equações paramétricas a partir dos pontos presentes na tabela chegaremos em algo parecido com isso:
Exercícios de Livros Relacionados
Uma haste, presa na origem do plano x y , ocupa a posição da reta que faz um ângulo de θ radianos com o eixo positivo dos x . A haste intercepta a reta y = 2 a no ponto A e a circunferência x 2 + y -
Uma haste, presa na origem do plano x y , ocupa a posição da reta x = t y . A haste intercepta a reta y = 4 no ponto S e a elipse 4 x 2 + y - 2 2 = 4 no ponto Q . Quando t varia, o vértice P do triâng
Uma haste, presa na origem do plano x y , ocupa a posição da reta x = t y . A haste intercepta a reta y = 4 no ponto S e a elipse 4 x 2 + y - 2 2 = 4 no ponto Q . Quando t varia, o vértice P do triâng
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.