Exercícios de Parametrizações Clássicas - Lista de Exercícios Resolvida

1 – Encontre uma parametrização para os seguintes círculos com centro em e raio :

1. e
2. e

2 – Encontre uma parametrização para as seguintes curvas:

Uma partícula se move a partir do ponto em cima da circunferência . Ela dá uma volta no sentido anti-horário, e depois duas no sentido horário. Parametrize a trajetória dessa partícula.

Dê a parametrização para cada uma das curvas:

1. A reta
2. A parábola
3. A circunferência
4. A elipse
5. O ramo da hipérbole
6. A reta

Seja o círculo de raio cujo centro é . Uma parametrização de com e , com parâmetro no intervalo , que percorre a curva uma vez no sentido anti-horário começando no ponto é tal que

Escolha uma opção:

, , , , e

, , , , e

, , , , e

, , , , e

, , , , e

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

Os vetores unitários que são paralelos à reta tangente à curva no ponto são:

Encontre todos os pontos em que a curva tem tangente horizontal, vertical ou não existente

Seja a curva dada por

1. Faça uma nova parametrização desta curva pelo comprimento de arco;
2. Demonstre através desta nova parametrização que o traço da curva é uma reta;
3. Obtenha uma nova representação paramétrica de uma forma onde e são dois vetores constantes.

Considere as superfícies

1. Exiba uma parametrização da curva espacial na forma

Explicitando , , , e .

Seja uma parametrização de uma curva, de classe , tal que velocidade e aceleração são linearmente independentes, contida no cilindro padrão . Prove a seguinte propriedade:

“O vetor normal associado à curva é sempre perpendicular ao eixo

do cilindro se e somente se a curva é equivalente a um movimento circular

ou helicoidal”

(Capítulo 13.2 – Exercício 3)

(a) Esboce o gráfico da curva plana com equação vetorial dada.

(b) Determine r’(t).

(c) Esboce o vetor posição r(t) e o vetor tangente r’(t) para o valor dado de t.

(Cap. 13.2 - Ex. 24) Determine as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado.

Determine a equação paramétrica da reta que passa pelos pontos e .

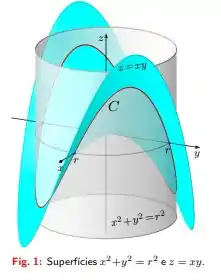
Seja a curva fechada dada pela interseção das superfícies de equações cartesianas e (Fig. 1).

Dê equações paramétricas para a reta tangente a no ponto .

1.1. Determine uma parametrização para as curvas dadas pela intersecção de:

d. O cilindro e o plano .

Uma partícula se desloca ao longo de uma curva descrita por:

Encontre a equação para uma superfície quádrica que contenha a curv. Identifique a quádrica.

4) Calcule a integral

Onde , .

O paraboloide intersecta o elipsoide ao longo de uma

curva C que contém o ponto Determine equações paramétricas para a reta tangente a no ponto .

Escreva uma curva parametrizada que passa por todos os pontos que satisfazem a equação:

Sejam os vetores em e e consideremos a reta .

1. Determinar os dois pontos da reta que têm distância da origem.

Transforme a equação polar em sua correspondente equação cartesiana:

a)

b)

c)

1.5. Seja , para .

a. Desenhe a imagem de , indicando o sentido de percurso.

1.5. Seja , para .

b. A imagem de está contida numa curva de nível da função dada por ? Em caso afirmativo, em qual nível?

1.1. Determine uma parametrização para as curvas dadas pela intersecção de:

a. O cilindro e a superfície .

1.2. Determine uma parametrização para as seguintes curvas:

a. ;

1.2. Determine uma parametrização para as seguintes curvas:

b. ;

1.2. Determine uma parametrização para as seguintes curvas:

c. ;

1.3. Verifique quais das curvas abaixo estão contidas na superfície . Verifique a sua resposta plotando, em algum software, a superfície e a curva num mesmo gráfico.

a.

1 – Parametrize a curva C definida por

E esboce duas de suas projeções nos planos coordenados.

1. Apresente uma parametrização diferenciável para as seguintes curvas planas:

Escreva uma curva parametrizada que passa por todos os pontos que satisfazem a equação:

para .

Esboce a imagem desta curva. O que acontece com esta imagem quando o valor

de varia?

A curva parametrizada por , está contida no plano:

Considere as seguintes curvas:

É correto afirmar que a imagem de

1. está contida na parábola
2. está contida numa circunferência de raio e centro em
3. está contida num ramo de uma hipérbole que passa em
4. está contida num ramo de uma hipérbole que passa em

A equação do plano que contém as duas retas parametrizadas por e é:

5. Não sei

Seja a curva dada por

1. Faça uma nova parametrização desta curva pelo comprimento de arco;
2. Demonstre através desta nova parametrização que o traço da curva é uma reta;
3. Obtenha uma nova representação paramétrica de uma forma onde e são dois vetores constantes.

1.1. Determine uma parametrização para as curvas dadas pela intersecção de:

b. O paraboloide e o cilindro parabólico .

1.1. Determine uma parametrização para as curvas dadas pela intersecção de:

c. O cone e o plano .

1.2. Determine uma parametrização para as seguintes curvas:

d. ;

Determine

Determine

Determine

Escreva a equação cartesiana da curva e faça um esboço indicando a direção na qual a

curva é traçada quando o parâmetro aumenta.

Dê uma parametrização para a curva:

O arco de menor comprimento do círculo

ligando os pontos

Escreva a equação cartesiana da curva e faça um esboço indicando a direção na qual a

curva é traçada quando o parâmetro aumenta.

Escreva a equação cartesiana da curva e faça um esboço indicando a direção na qual a

curva é traçada quando o parâmetro aumenta.

Escreva a equação cartesiana da curva e faça um esboço indicando a direção na qual a

curva é traçada quando o parâmetro aumenta.

Dê uma parametrização para a curva:

A elípse

Dê uma parametrização para a curva:

A reta

Dê uma parametrização para a curva:

O círculo

Dê uma parametrização para a curva:

O segmento de reta ligando os pontos

Seja a curva com equações paramétricas

Determine uma parametrização da reta tangente à curva no ponto ;

Seja a curva com equações paramétricas

e reta tangente à curva no ponto dada por

Calcule a reta ortogonal a no ponto

Seja a curva com equações paramétricas

Esboce a curva

Uma partícula se move ao longo de uma curva

Se o vetor velocidade da partícula é dado por

Calcule o vetor posição da partícula

Dê uma parametrização para a curva

A parábola com vértice , foco e diretriz .

(Dica: Uma par��bola com foco e reta diretriz , é constituída de todos os pontos

cuja distância a e a são iguais. A distância de um ponto à é

a distância de ao ponto em mais perto de . Deduza do Teorema de

Pitágoras, que ponto é este.)

Seja a curva com equações paramétricas

Calcule sem usar as equações cartesianas

Uma partícula se move ao longo de uma curva

ache a expressão do vetor velocidade da partícula

Se a partícula, no instante , passa pelo ponto , determine os valores

das constantes que aparecem no item anterior.

Suponha que a posição de duas partículas no instante t seja dada por ,

, respectivamente.

Ache as equações cartesianas das duas trajetórias;

Suponha que a posição de duas partículas no instante t seja dada por ,

, respectivamente.

Trace as trajetórias de ambas as partículas;

Suponha que a posição de duas partículas no instante t seja dada por ,

, respectivamente.

Quantos pontos de interseção existem?

Suponha que a posição de duas partículas no instante t seja dada por ,

, respectivamente.

Existe colisão entre as partículas?

Seja P um ponto a uma distância do centro de uma roda de raio , que gira sem deslizar

sobre o eixo . Reproduzindo o esquema que usamos para parametrizar a ciclóide (caso

em que ), mostre que a curva descrita pelo ponto , chamada trocóide, tem equações

paramétricas

Verifique que a curva parametrizada por , , é plana.

Verifique que a trajetória , , é uma curva lisa cuja trajetória está contida na interseção do cilindro circular reto com a esfera . Esboce e e destaque a trajetória de .

Seja a função . Verifique que parametriza a curva interseção das superfícies e . Que superfícies são essas? Esboce-as e destaque a trajetória de . Destaque os pontos .

Em que ponto as curvas e se interseptam? Determine o ângulo entre elas no ponto de interseção.

Esboce cada curva parametrizada a seguir e determine seu comprimento.

(b) A espiral logarítmica com

Considere o cilindro circular reto e o plano . Obtenha uma parametrização para a curva correspondente à interseção e esboce, em uma mesma figura, o cilindro e o plano , destacando a trajetória da curva .

Considere a espiral , , e a circunferência de equação .

(a) Determine o instante e o ponto em que a trajetória de intersepta .

Considere a espiral , , e a circunferência de equação .

(c) Quantas voltas completas ao redor da origem descreve a trajetória de antes de tocar ?

Considere a espiral , , e a circunferência de equação .

(d) Desenhe a trajetória de e a circunferência , destacando a interseção entre elas.

Considere a curva parametrizada por , com .

(a) O ponto de interseção da trajetória de com o plano .

Esboce cada curva parametrizada a seguir e determine seu comprimento.

(a) com

Esboce cada curva parametrizada a seguir e determine seu comprimento.

(c) A catenária com . Lembre-se:

Uma partícula se move no plano segundo o vetor posição .

(a) Verifique que a trajetória está sobre a parábola e desenhe a trajetória.

A função posição de uma partícula é dada por . Determine o instante em que sua velocidade escalar é mínima. Qual é a velocidade escalar mínima?

Uma partícula se move no plano segundo o vetor posição .

(b) Quais são os vetores aceleração nos instantes de velocidade zero? Desenhe estes vetores.